Linear Algebra 2

Office Hours

• Wed 6:30pm - 7:30pm
• Fri 5:30pm - 6:30pm

Schedule

Notes

• All quizes based off homeworks
• Best 4/5 quizzes
• Quizzes start from week 3 in tutorial
• All computations should have whole numbers or Complex Number, but they should be easy
• 30% (4-6hrs per week) understanding basic defn, terms, computations. This is the most important
• 60% (1-2hrs per week) understanding problems from class and most homeworks
• 80% (1-2hrs per week) understanding what is presented
• Late submission policy after 4 days
• 30-40% of the assesments will be using the definitions, prove these basic properties…
• There is a bonus quiz 6, which will be the material after quiz 5. It is extra material
• The quiz will require you to reform numbers to match the Finite Field. E.g, in $\mathbb{Z}\mathrm{mod}5$, $(x-2)=(x+3)$
• Characterization of Triangularizability and Diagonalizability in Terms of the Minimal Polynomial is a very important theorem for the final
• Companion Matrix is on the exam

Concepts

Week 0.1

• Field
• Integer Modulo n
• Finite Field
• Congruent Modulo
• Equivalence
  • Reflexive
  • Symmetric
  • Transitive
• Modulus
• Uniqueness Field Properties

Week 1.1

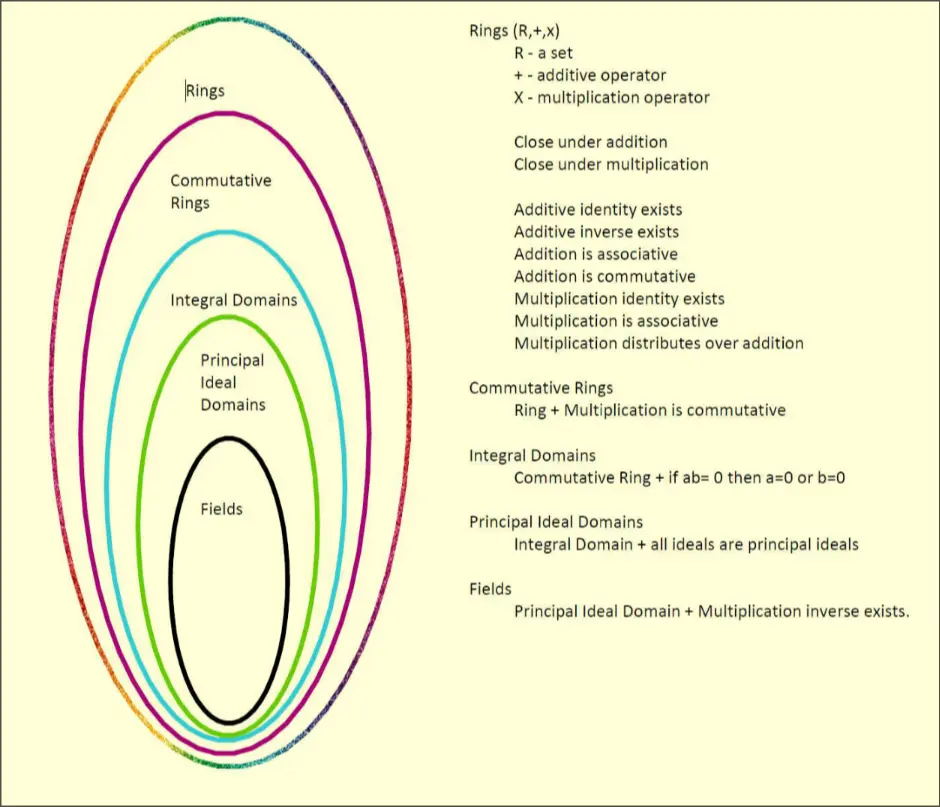
• Ring
• Commutative Rings
• Integral Domain
• Principle Ideal Domain
• Euclidean Domain
• Additive Subgroup
• Ideal
• Field

Week 1.2

• Generator for Ideal
• Euclid’s Algorithm to find GCD
• Remainder Theorem
• Polynomial Ideal
• Vector Space
• Linear Combination
• Span
• Linear Independence
• Basis

Week 2

• Vector Space
• Subspace
• Spanning Set
• Linear Independence

Week 3

• Swap Operator
• Permutation Notation
• Standard Basis Matrix
• Vector Space Isomorphic
• Ordered Basis
• Linear Operator

Week 4

• Change of Basis
• Linear Functional
• Perpendicular Set
• Standard Inner Product
  • Standard Inner Product for Complex Numbers
  • Standard Inner Product for Real Numbers
• Riesz Representation Theorem
• Annihilator
• Error Correcting Codes

Week 5.1

• XOR Encryption
• Metric
  • Euclidean Metric for Complex Numbers
  • Euclidean Metric for Real Numbers
  • Metric for Integer modulo n
• Norm
  • Absolute Function
  • Complex Number Modulus
  • Trivial Absolute Value
• Metric for Vector Spaces
• Nice Metric
• Vector Norm

Week 6

• Transform Norm
• Matrix Norm
• Standard Inner Product
• Standard Inner Product for Vector Spaces
• Inner Products Define a Norm
• Polarization Identity
• Inner Product Space

Week 7

• Generalized Pythagorean Theorem
• Perpendicular Set
• Orthogonal Set
• Orthonormal Set
• Fourier Basis
• Orthogonal Sets are Linearly Independent
• Orthogonal Sets to Find Coordinates
• Matrix Representations of Linear Map with Respect to Orthonormal Basis
• Gram-Schmidt Algorithm
• Best Approximation
• Orthogonal Projection
• Orthogonal Complement
• Bessels Inequality
• Orthogonal Subspace
• Change of Basis with Orthonormal Basis

Week 8

• Least Squares Method
• Least Squares Theorem
• Line of Best Fit
• Adjoint
  • Adjoints Exist for Finite Dimensional Space
• Matrix Representations of Linear Map with Respect to Orthonormal Basis
• Matrix Representation of Adjoints with Respect to Orthonormal Basis
• Hermitian Matrix
• Pauli Matrices
• Preserving Inner Products and Vector Isomorphism
• Unitary Operator
• Orthogonal Matrix
• Orthonormal Matrix
• Diagonal Operation
• Normal Operator
• QR Factorization

Week 9

• Complex Inner Product Space
• Superposition
• Quantum Operation
• Normal Operator
• Normal Matrix
• Upper Triangular Matrices are Normal If and Only if They are Diagonal
• Invariant
• Invariant Under Adjoint
• Schur’s Decomposition
• Unitarily Upper Triangular
• Unitarily Diagonizable
• Spectral Theorem for Normal Operator
• Spectrum of a Matrix
• Relationship between Trace, Determinant and Eigenvaues
• The Spectrum of Unitary Operators on a Complex Inner Product Space lies on the Unit Circle
• Spectral Theorem for Unitary Operators
• Spectral Theorem for Unitary Matrixes
• Eigenvectors for Different Eigenvalues are Orthogonal for Symmetric Matrixes --- Midterm content ends here
• Polynomials over a Field
• Polynomial
• Polynomial Function
• Applying Polynomials to Linear Operators
• Polynomial Ideal
• Division Algorithm for Polynomials
• Fundamental Remainder Theorem
• Division Algorithm for Integers
• Reducible Function
• Reducible Polynomial
• FTOA
• Prime Factorization of Polynomials
• Fundamental Theorem of Algebra

Week 10

• Finitely Generated Polynomial Ideal
• Principle Polynomial Ideal
• Polynomial Ideal Fx is a Principle Ideal Domain
• Greatest Common Divisor of Polynomials
• Euclidean Algorithm for Integers
• Euclidean Algorithm for Polynomials
• Polynomial Field
• Finite Fields Have a Multiplicative Inverse
• Creating a Field from a Principal Ideal Domain
• Conductor

Week 11

• Proper Subspace Can be Multiplied to Be Within Other Subspace Lemma
• Invariant Subspace
• Set of Triangular Matrixes
• Invariant Subspace Characterization of Triangularability
• Characterization of Triangularizability and Diagonalizability in Terms of the Minimal Polynomial
• Every Complex Operator is Triangularizable
• Determine if Matrix is Triangularizable or Diagonalizable
• Matrix Definition of Cyclic Subspace
• Block Diagonal Matrix
• Independent Subspaces
• Distinct Eigenvalues Imply Eigenspaces are Linearly Indepedent
• Projection
• Projections from Direct Sum Theorem
• Direct Sum of Linear Transformations
• Diagonalizable Properties Theorem
• Using Lagrange Polynomial to Compute Eigenspace

Week 12

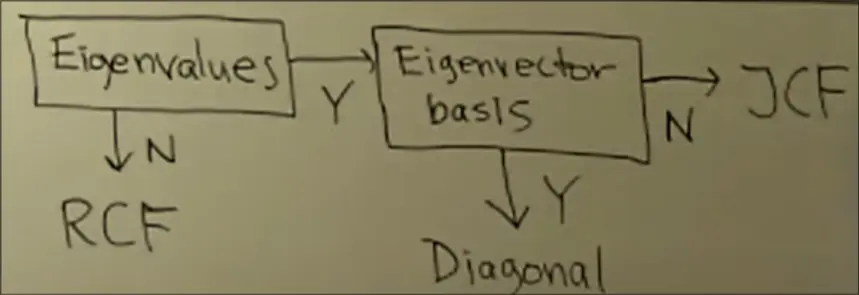
• T-Annihilator of a Vector
• A Vector exists with T-Annihilator Equal to the Minimal Polynomial
• Primary Decomposition Theorem
• Cyclic Decomposition Theorem
• Jordan Matrix
• Jordan Form
• Rational Form