Computing Kernels

The kernel is the set of inputs for $T:V\to W$ that result in $\overrightarrow{0}$ as the output.

1. Find the Matrix Transformation $A$
2. Solve for the Column Vectors $x$ in $Ax=\overrightarrow{0}$

Example 2

Compute kernel of the transformation:

• $T_1:{\mathbb{R}}^3\to {\mathbb{R}}^3$ projection to x-axis

Soln

• Example $T_1$
• In coordinates it is: $T_1(x,y,z)=(0,0,z)$

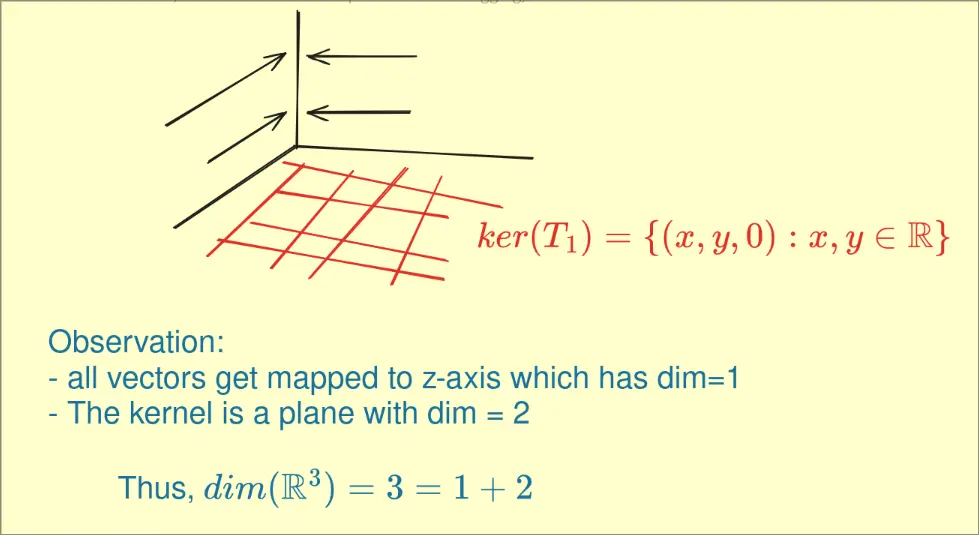
Example 3

• $T_2:{\mathbb{R}}^2\to {\mathbb{R}}^2$ rotation to $\theta =\frac{\pi }{2}$

Soln

• Example $T_2$

\left[\begin{array}{cc} 0 & -1 \ 1 & 0 \ \end{array}\right] \left[\begin{array}{cc} x\ y\ \end{array}\right] = [-y,x]

Thus, $ker(T_{2}) = \{ (0,0) \}$