A method of thinking to view problems as boxes and occupants.
Example question
How many 5 digit odd numbers can be formed with the digits: 1,2,3,4,5?
We can think of digits as boxes
5 digits.
There are 3 possible occupants for the last box: 1,3,5.
Now, it doesn’t matter order of the other numbers are, just that you dont repeat a digit.
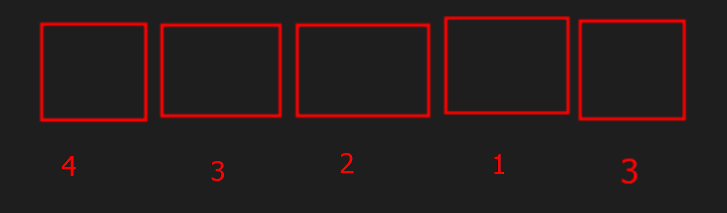4*3*2*1*3 = 72
4 digits possible for first box, since at the moment, 1 is reserved at the end.
3 digits possible for 2nd box since 1st and last are already reserved
so on so forth for 3rd box and 1st box.
Another one
Question: How many ways can a president and vice-president be selected from 6 people?
First box is president, once the first box has a person, there are only 5 people the vice president can be.
Clumping boxes
Oftentimes, questions will say things like: These 2 people must sit next to eachother, these 2 bacteria are always paired. In cases like that, it would be wise to group those 2 boxes together. and multiply the permutations that clumped box can have with the wider box permutations as well.
For example, 5 people sitting. 2 people must sit together.
Find people
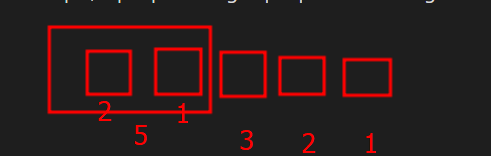so it is 5*3*2*1 * 2! = 60