Logarithms

Table of Contents

Logarithm

A logarithm is equal to an exponent 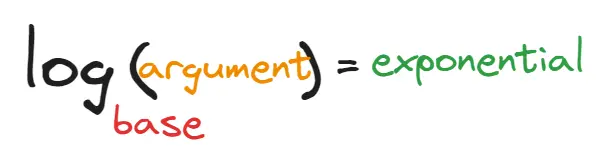Logarithms are the function that gets you the power from given a base and a result 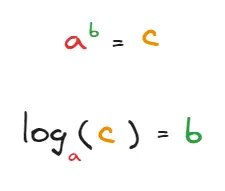Base: $0<x<1\cup x>1$ Argument: $0<x$ Exponential: $x\in R$

Log Properties

only valid if b is positive ${\log }_b(1)=0$ ${\log }_b(b)=1$ ${\log }_b(b^x)=x$ $b^{{\log }_{b}x}=x$ $e^{\ln x}=x$ $lo{g}_{b}x=\frac{1}{{\log }_{x}b}$

Logs ARGUMENT never be negative

Because, base^2 can NEVER be negative A log is an exponent. remember

Log Bases never be negative

A log is an equation(sorta). Its saying that the argument^exponential can equal to the argument. You provide it the base and argument, it returns the exponential.

The problem is when you give it a argument that the base can never equal. eg: ${\log }_{-2}(8)$ $(-2{)}^x=8$ ^ This will never be true. Unless you use Imaginary Number

Log Base can NEVER BE One

Because, 1^anything = 1. Which is saying you will have infinite y-values for one x value. You cant return anything

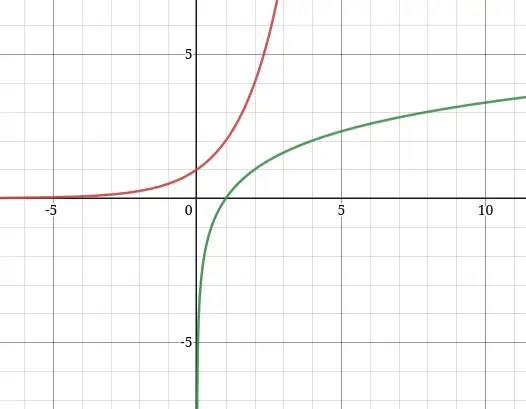
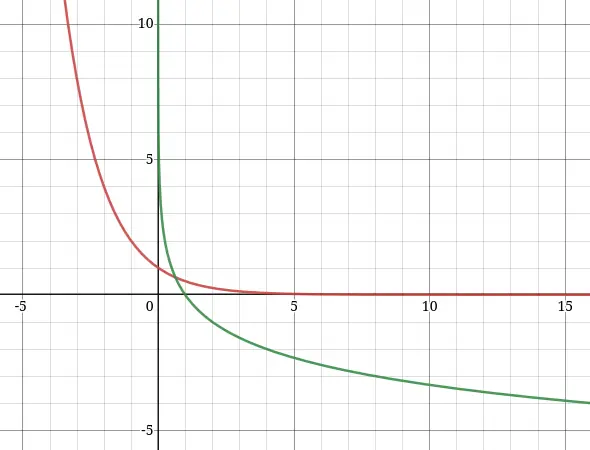
Inverse Exponentials

If you graph out a logarithm function of any base, like $y={\log }_{a}x$ then, it will look like a inverse Exponential Functions graph

Inverse of Growth

$y={\log }_{a}x$

Inverse of Decay

$y={\log }_{\frac{1}{a}}(x)$

Natural Logarithms

ln is that function which can help you with logarithms of different bases. it uses eulers number $e$ as the base. Golden ratio shenanigans

Theorems

Change of Base Theorem

$\frac{\log t}{\log b}={\log }_{b}t=x$

Power Law

${\log }_b(x^n)=n{\log }_{b}x$

Product Law of Logarithms

${\log }_b(mn)={\log }_{b}m+{\log }_{b}n$

Quotient Law of Logarithms

${\log }_b(\frac{m}{n})={\log }_b(m)-{\log }_b(n)$

Graphing Logarithms

Famous 5(Depends on Base)

x	y
base^-2	-2
base^-1	-1
base^0	0
base^1	1
base^2	2

Example With Transformation

Graph y = log(x-2)-5

1. Get the mapping rule (x+2,y-5)
2. Get the V.A. in this case it is x = 2
3. use Graphing Logarithms famous five

x	y
10^-2	-2
10^-1	-1
10^0	0
10^1	1
10^2	2
with mapping rule (x+2,y-5)

x+2	y-5
2.01	-7
2.1	-6
3	-5
12	-4
102	-3
You can use decimals. Dont do shit like 10^-2+2, make them decimal

4. Y intercept? X intercept?
5. Domain? Range?(usually Y∈ℝ)