WHEN THE DENOMINATOR… IS A QUADRATIC
Translations
Horizontal Shift.
This shift:
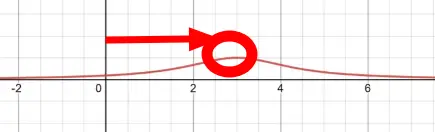Is based on the vertex of the original graph.
It uses the same 1/vertex principle as the other quadratic reciprocal graphs do.
Quadratic Reciprocal With No Roots
reciprocal of this function would be like this:
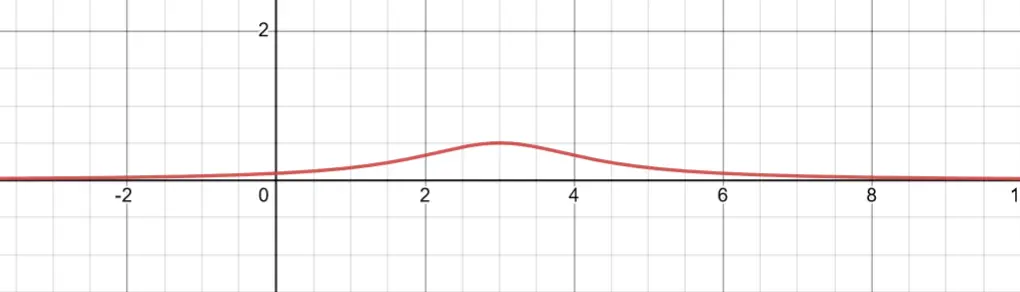As there is no roots, the denominator will never be zero, meaning there are no restrictions for x.
Thus:
**The domain is always X ∈ ℝ,
as
as
V.A: None
H.A: y = 0
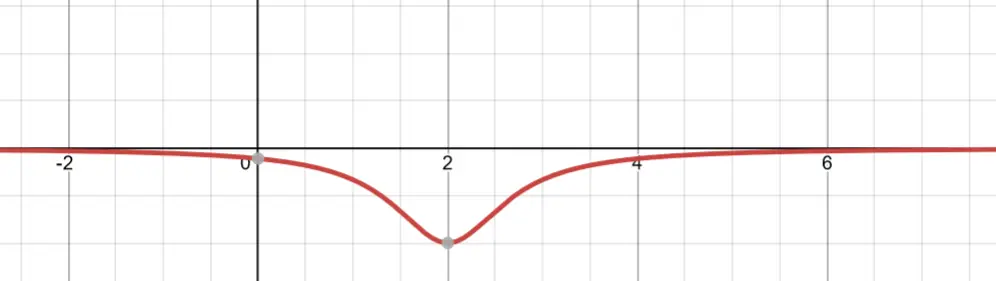
Flipped
Of course, you can also have a negative reciprocal function to result in a flipped graph
Quadratic Reciprocal with One Root
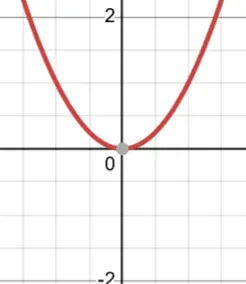In cases where you have a quadratic equation like f(x) =
your reciprocal g(x) will look like g(x) =
and it will have a vertical asymptote since x can have a zero root
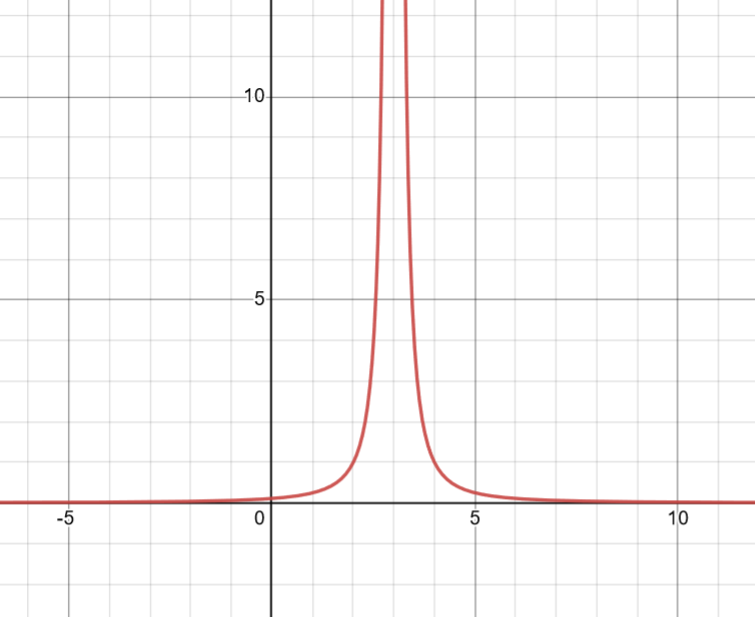also with the horizontal asymptote too at y = 0.
V.A = 3
roots of x
Quadratic Reciprocal with Two Root
if a quadratic function has 2 roots, the reciprocal function will look fragmented.
if f(x) = (x-2)(x+3)
then it has 2 roots
g(x) = 1/f(x) will look like:
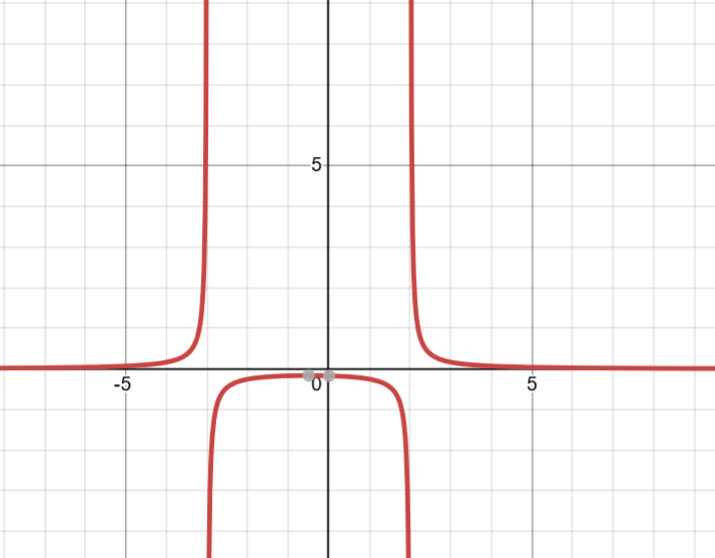H.A = 0
V.A = 2, -3
To map the Behavior of Reciprocal for this, you will have to test for each of these roots. find when approach left, approach right for both these roots
Maxima Minima → Mapped
This ‘thing’
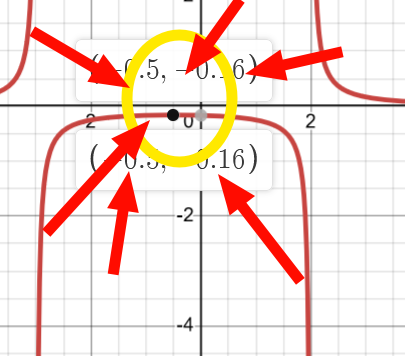corresponds to the reciprocal of maxima/minima of the original function f(x)
OR also, the middle between the 2 vertical asymptotes
Domain and range
Domain: {x∈ℝ, x!=-3, x!= 2} Range: {y∈ℝ, y > 0, y ≤ -0.16}
Range is the tricky one, you list 2 intervals.