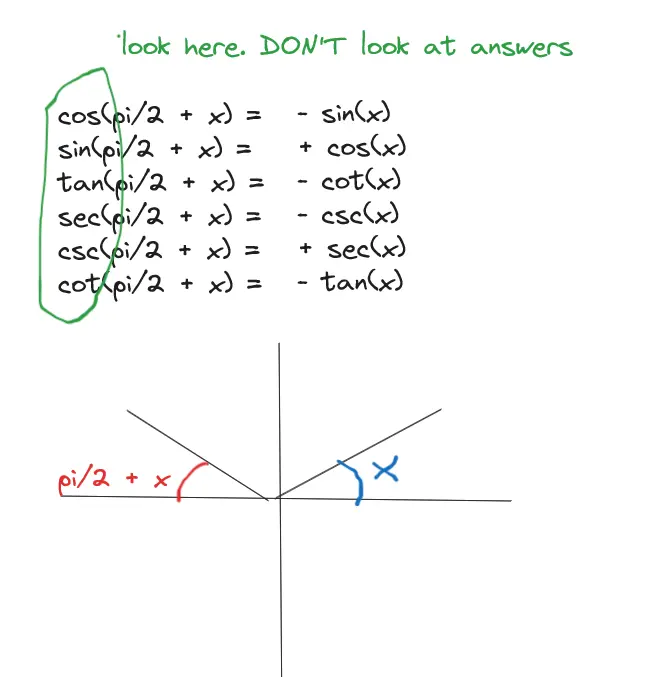
Derivation
A trig identity based on Complementary Angles
If we have a right angle triangle, the angles must add up to 180
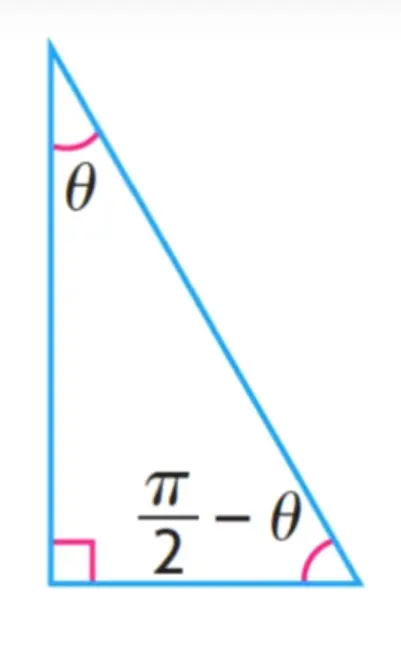 Since we already used a 90 degree angle, we are left with theta. the complementary angle finishes it.
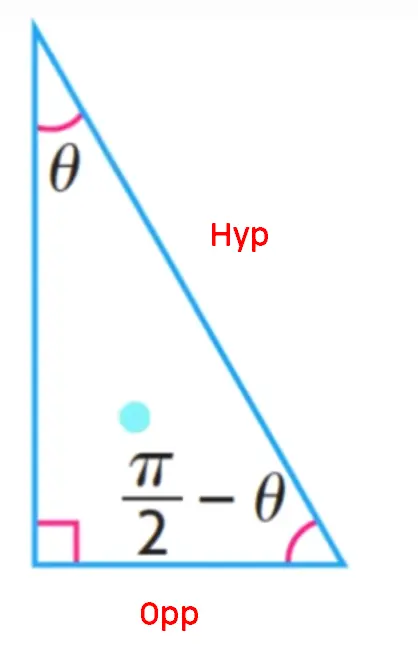
The sin of theta would be using these 2 lengths
Since we already used a 90 degree angle, we are left with theta. the complementary angle finishes it.
The sin of theta would be using these 2 lengths
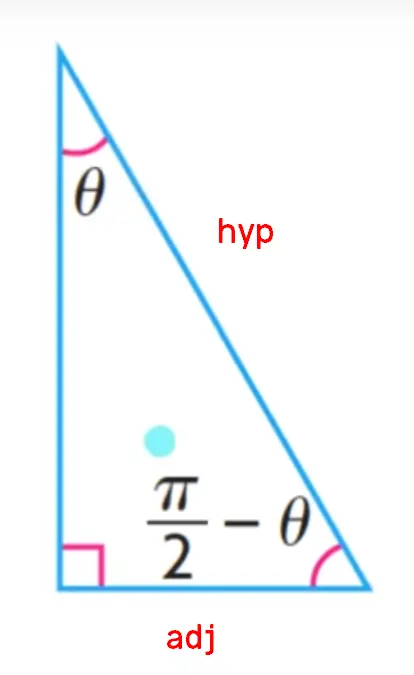
 The cos of theta’s complement would be using these 2 lengths as well.
The cos of theta’s complement would be using these 2 lengths as well.
 angles that are complements of each other will have the same sine → cosine and same cosine → sine.
Such is visible in the unit circle as well. a few trig ratios in the same quadrant have the same values, just in reverse order.
angles that are complements of each other will have the same sine → cosine and same cosine → sine.
Such is visible in the unit circle as well. a few trig ratios in the same quadrant have the same values, just in reverse order.
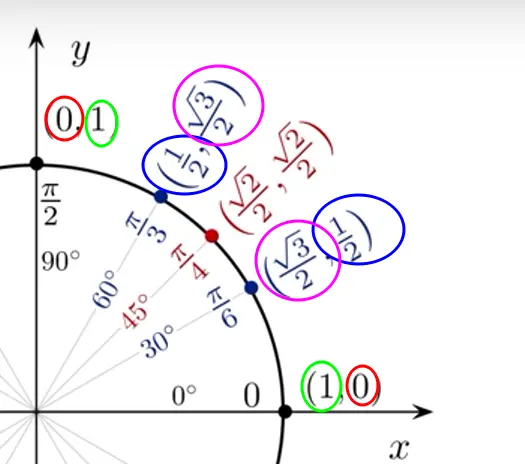 The sin of is the cos of
The sin of is the cos of
The sin of is the cos of
The sin of is the cos of
Thus, we can say the
Identities
To find identities, one must be willing to draw the quadrants, and predict. You have 3 possible ways the trig function can look: You can do all 3 of them, or one of them
If x is provided, use x. If x is not provided, assume x = 30, then figure out.
lets do it for one of them.
- Draw out the list of functions like such:
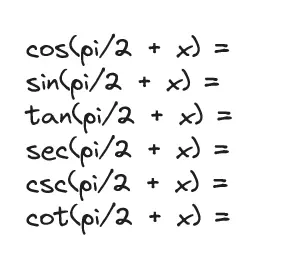
- Make each function equal its opposite version

- As x was not provided, we must assume x = 30.
 Now fill in the chart as where the transposed angle ended up(in the second quadrant).
Now fill in the chart as where the transposed angle ended up(in the second quadrant).