Tools for analyzing situations where there is overlap among sets.
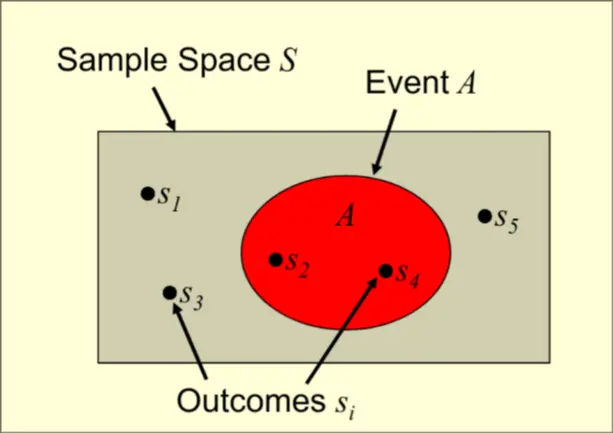
- Outcomes are expressed as dots
- Events are expressed as a collection of dots
- Sample Space is rectangle
Example
Rolling a 6-sided dice:
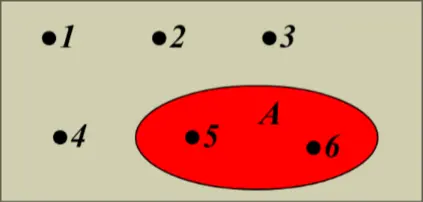
Common Elements
elements in one set, being in another set as well
 The symbol for element of is: ∈
X ∈ R, remember?
The symbol for element of is: ∈
X ∈ R, remember?
Subsets
when all the elements of one set are also elements of another set. If all elements of set C are also elements of set A, then C is a subset of A
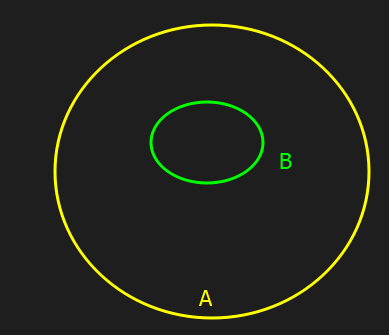 The set itself is a subset of itself. weird.
The subset symbol is: ⊆
B ⊆ A
The set itself is a subset of itself. weird.
The subset symbol is: ⊆
B ⊆ A
Universal Set
Venn diagrams often have 1 box around them, this box represents the universal set S Every set is a subset of the universal set.
Principle of inclusion and exlcusion
n(A or B) = n(A) + n(B) - n(A and B) n(A∪B) = n(A) + n(B) - n(A∩B) the set of all elements in either set a or set b is the Union of A and B. similarly, the set of elements inside A AND B, is the intersection
Sample questions
2 Sets
11 Farce actors, 7 actors in Molière. 3 actors in both plays. How many students are in ONLY one play.
Understand that 3 of the 11 farce and 3 of the 7 Moliere belong to both. Draw the diagram a such:
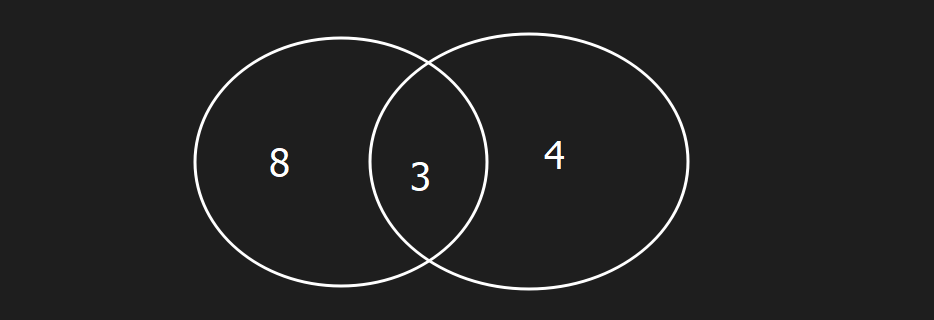 so, 8 + 4 = 12
so, 8 + 4 = 12
3 Sets
140 students in high school. 52 in biology, 71 in chemistry, 40 in physics. 15 take both bio and chem, 8 take both bio and physics, 11 take both bio and physics, 2 are taking all 3. How many students are not taking any of these 3 science courses?
we need for find n(B∪C∪P).
Start with a boilerplate Venn diagram
 Firstly, we know there are 2 people taking all 3.
Firstly, we know there are 2 people taking all 3.
 Then, the second intersections. 15 take both bio and chem, 15 -2 = 13. do same for others.
Then, the second intersections. 15 take both bio and chem, 15 -2 = 13. do same for others.
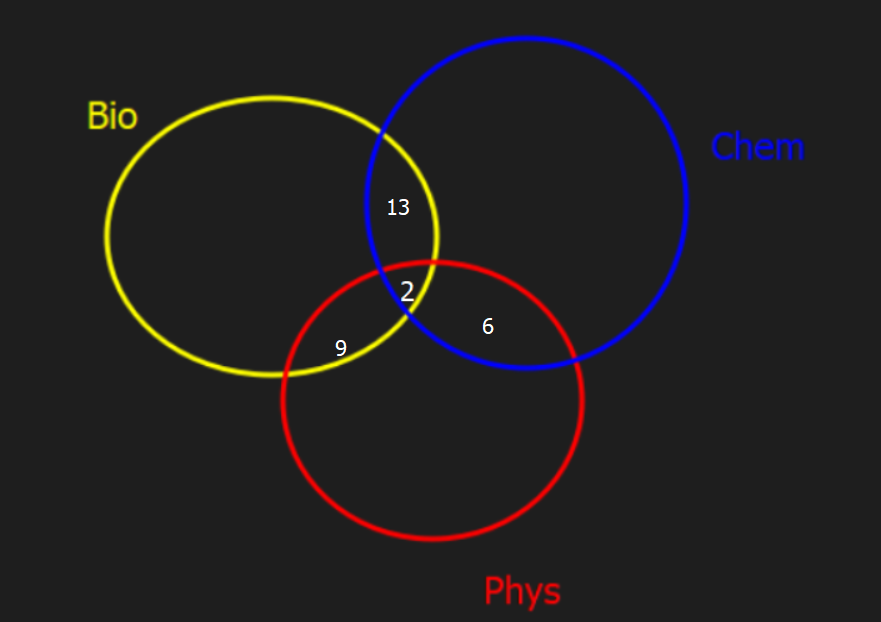 Lastly, there are 52 for bio, 52 - 9 - 13 - 2= 28. same for others too.
Lastly, there are 52 for bio, 52 - 9 - 13 - 2= 28. same for others too.
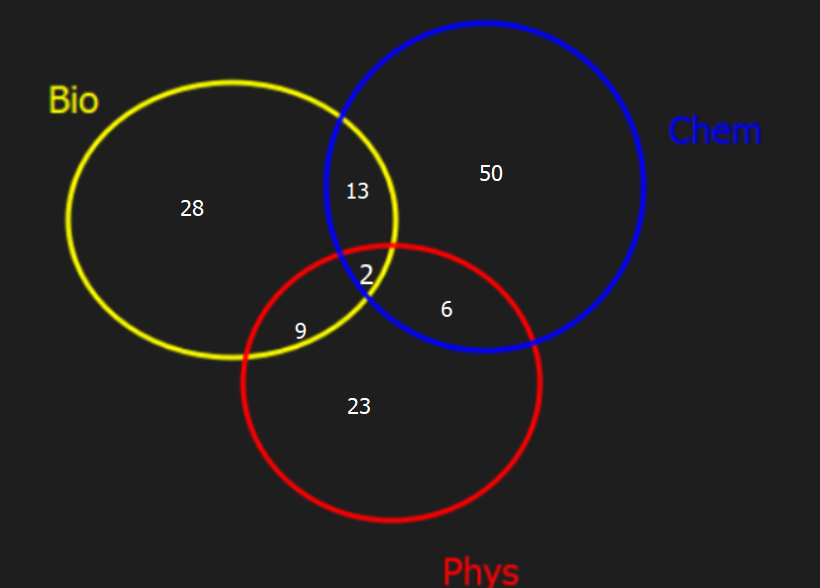 Now, to find out how many people are not taking, count the # of people who are. add every number we got. 28+23+50+9+6+13+2 = 131.
140 - 131 = 9
there are 9 people who are not taking.
Now, to find out how many people are not taking, count the # of people who are. add every number we got. 28+23+50+9+6+13+2 = 131.
140 - 131 = 9
there are 9 people who are not taking.

n(B∪C∪P) = n(B) + n(C) + n(P) - n(B∩C) - n(C∩P) - n(P∩B) + n(A∩C∩P)
Add the singletons, subtract the doubletons, add the tripletons, subtract the quadtons if there are any. its alternating. so, you know what we do with quintons, we add. ADD the odds, Subtract the evens.