Euclidean Metric for Complex Numbers

Definition

• With $x_1,x_2\in \mathbb{C}$
• Let $x_1=a+bi$
• Let $x_2=c+di$
• Let $d(x_1,x_2)=\sqrt{(a-c{)}^2+(b-d{)}^2}$

Proof by Metric Axioms

Proving $d(x,y)\ge 0$

• Let $x,y\in \mathbb{C}$
• Then, $x=a+bi$ and $y=c+di$
• $d(x,y)=\sqrt{(a-c{)}^2+(b-d{)}^2}$
• Note that $(a-c{)}^2\ge 0$ by ineq prop of $(\cdot {)}^2$
• Note that $(b-d{)}^2\ge 0$ by ineq prop of $(\cdot {)}^2$
• Then, note that $(a-c{)}^2+(b-d{)}^2\ge 0$ by ineq props
• So, this $\sqrt{(a-c{)}^2+(b-d{)}^2}$ is defined for all $x,y$
• Note that $\sqrt{\cdot }$ has a range of $[0,\infty )$
• Thus, $d(x,y)\ge 0,\forall x,y$

Proving $d(x,y)=d(y,x)$

• Let $x,y\in \mathbb{C}$
• Then, $x=a+bi$
• Then, $y=c+di$
• With L.S = $d(x,y)=d(a+bi,c+di)=\sqrt{(a-c{)}^2+(b-d{)}^2}$
• $=\sqrt{(c-a{)}^2+(b-d{)}^2}$
• $=d(c+di,a+bi)=d(y,x)$
• Thus, $d(x,y)=d(y,x)\forall x,y\in \mathbb{C}$

Proving $d(x,y)=0⟺x=u$

Proving $⟸$

• Let $x=y\in \mathbb{C}$
• Then, $x=y=a+bi$
• Then, $d(x,y)=d(a+bi,a+bi)=\sqrt{(a-a{)}^2+(b-b{)}^2}=\sqrt{0}=0$

Proving $⟹$

• Let $x,y\in \mathbb{C}$ s.t $d(x,y)=0$
• Then, $x=a+bi$
• Then, $y=c+di$
• Suppose for sake of Contradiction that $x\ne y$
• Then, either $a\ne c$ or $b\ne d$
• Then, this means $a-c\ne 0$ or $b-d\ne 0$
• This means $(a-c{)}^2>0\wedge (b-d{)}^2\ge 0$ or $(b-d{)}^2>0\wedge (b-d)\ge 0$
• This implies that $(a-c{)}^2+(b-d{)}^2>0$
• This implies $\sqrt{(a-c{)}^2+(b-d{)}^2}>0$
• This implies $d(x,y)>0$
• Contradicts that $d(x,y)=0$
• Thus, $x=y$ by contradiction

Proving $d(x,z)\le d(x,y)+d(y,z)$

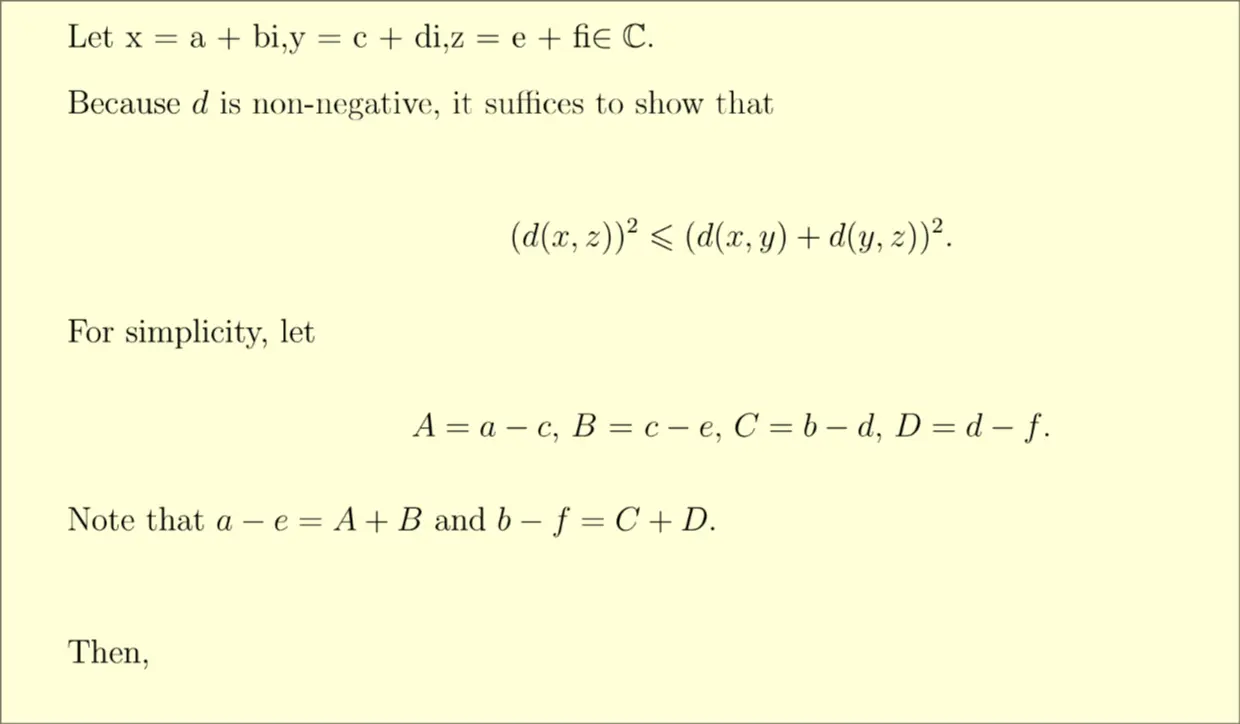
Proof from defintion of Norm

Note that our definition of a metric follows from the Absolute Function for Complex Numbers and Absolute Value Functions Induce a Metric Theorem so it follows that this is the correct metric