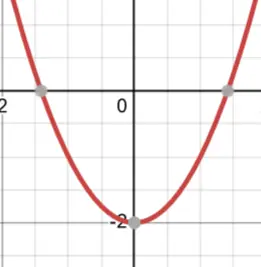
if a quadratic function has 2 roots, the reciprocal function will look fragmented.
if f(x) = (x-2)(x+3)
then it has 2 roots
g(x) = 1/f(x) will look like:
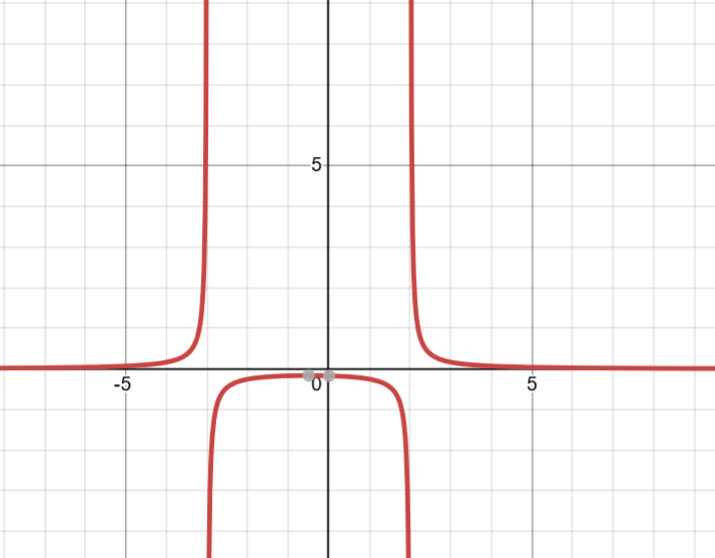H.A = 0
V.A = 2, -3
To map the Behavior of Reciprocal for this, you will have to test for each of these roots. find when approach left, approach right for both these roots
Maxima Minima → Mapped
This ‘thing’
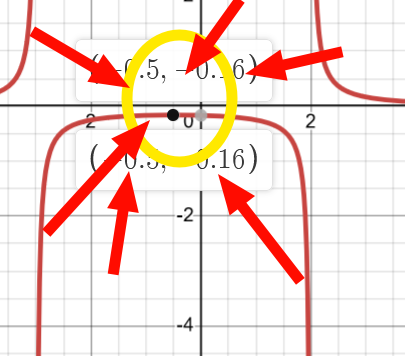corresponds to the reciprocal of maxima/minima of the original function f(x)
OR also, the middle between the 2 vertical asymptotes
Domain and range
Domain: {x∈ℝ, x!=-3, x!= 2} Range: {y∈ℝ, y > 0, y ≤ -0.16}
Range is the tricky one, you list 2 intervals.