Rules of Inference

Figures out what is true from something else. To show that two arguments are equivalent, we could use a Truth Table, but we could also use Deductive Reasoning.

If an argument is valid, if the conclusion if valid. using the rules of inference you can prove the statement is a Tautology.

Rules

Addition

If I have P is true, then i know that P OR whatever is true $P⟹P\vee Q$

Simplification

If both $P\wedge Q$ are true, then: $(P\wedge Q)⟹P$

Modus Ponens

$(P\wedge (P⟹Q))⟹Q$ If P is true, and P implies Q, then you can conclude Q.

Modus Tollens

$((P⟹Q)\wedge \neg Q)⟹\neg P$ Derived from Contrapositive Statement

Hypothetical Syllogism

$((P⟹Q)\wedge (Q⟹R))⟹(P⟹R)$ A statement proving a child statement, will prove that child’s child aswell.

Disjunctive Syllogism

$((P\vee Q)\wedge \neg P)⟹Q$ P or Q is true. if one of the terms is false, then the other must be true

Conjunction

$(P\wedge Q)⟹(P\wedge Q)$ Self explanatory

Resolution

$((P\vee Q)\wedge (\neg P\vee R))⟹(P\vee R)$

Rules for Quantified Statements

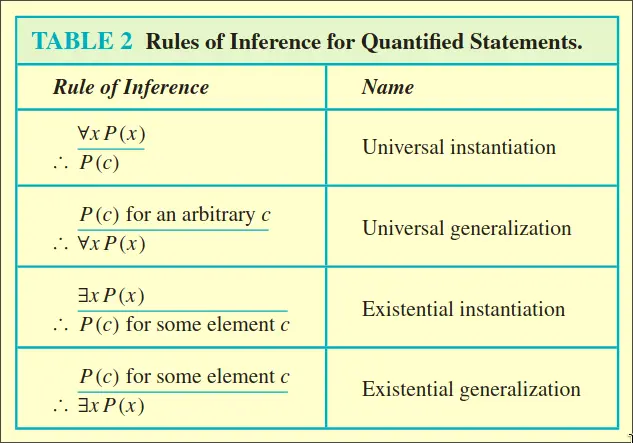If you instantiate a existence before a universal instantiation, then you cannot use the same instantiated existance variable before for the universal instantiation

Universal Instantiation

If we show that a function works for all numbers, then we can sub in an arbitrary number into the function

Universal Generalization

If an arbitrary number can be subbed into P(x), then P(x) work for all values of x. You must use a fresh new variable that did not appear in the argument/proof.

Existential Instantiation

If there exists an element c, then c cannot be arbitrary and there is one value c where P(c) is true

Existential Generalization

If there is a value c that allows P(c) to be true, then we know there exist a c to allow P(c) to be true.

Rules of Inference

Simple Induction

1. P(b)
2. $\forall k\ge b,P(k)⟹P(k+1)$ Therefore, $\forall n\ge b,P(n)$

Strong Induction

1. $\forall k\ge b(\forall b\le i<k,P(i)\to P(k))$ Therefore, $\forall n\ge b,P(n)$