Using pascal triangle to save some time calculating the ways you can get to each node in a route.
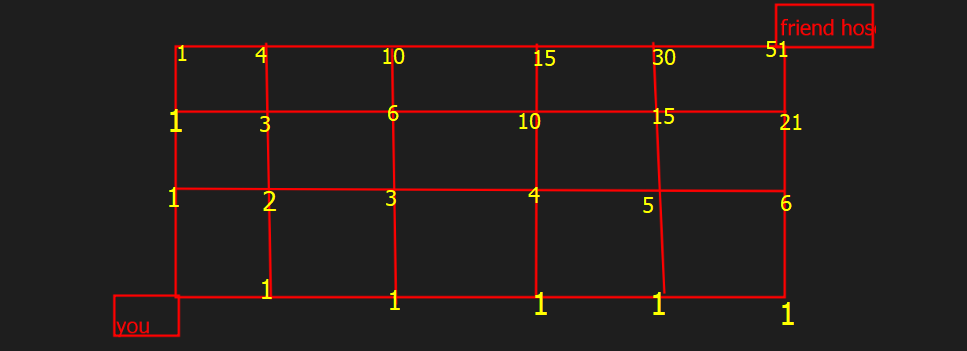
House Route example
 We want to know how many ways there are to get to your friends house.
You can only go either left or right.
So, for each node you will draw the possible ways to get to it.
We want to know how many ways there are to get to your friends house.
You can only go either left or right.
So, for each node you will draw the possible ways to get to it.
Checkers game
We can only move our piece diagonally. The goal is to move to the final row. How many ways can we make it there?
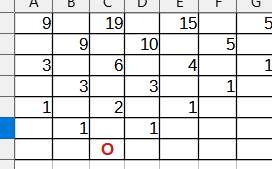 we have all the cases now, and then add the Mutually Excusive last row. it is equal to 48.
Now, say we put a barricade in the middle.
we have all the cases now, and then add the Mutually Excusive last row. it is equal to 48.
Now, say we put a barricade in the middle.
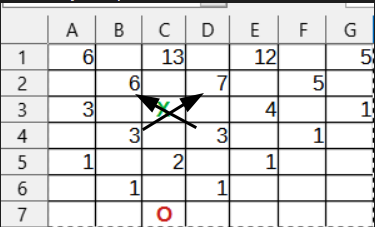 We would just assume the path before the blockade is added.
again. count the last row, there are 36. A lot less possibilities.
We would just assume the path before the blockade is added.
again. count the last row, there are 36. A lot less possibilities.