Determinant

A matrix operation that is useful for determining scale factor that a transformation has on the area of the ‘paralellogram’ created by a linear transformation on its basis vectors.

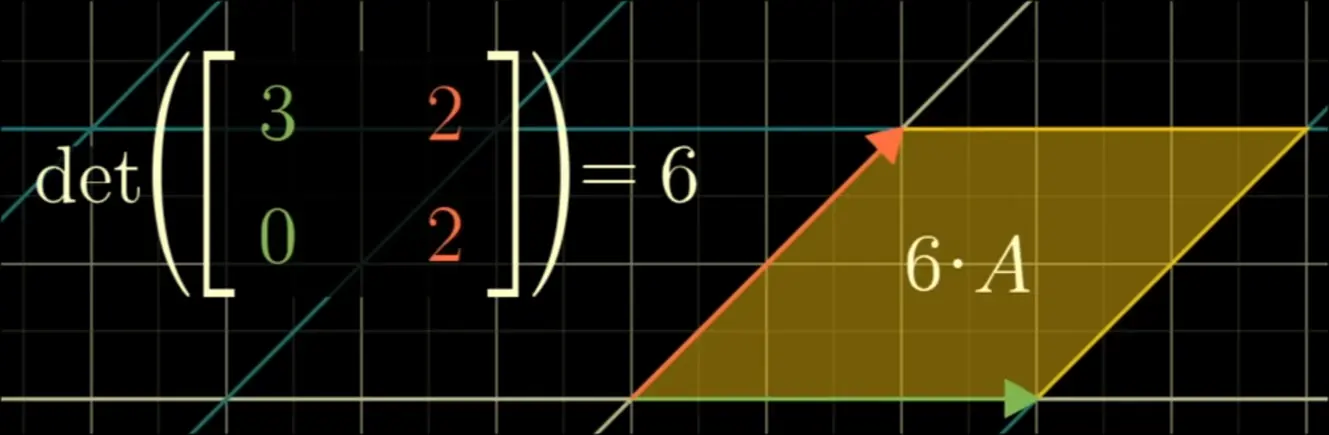
Definition

The determinant is the alternating Multilinear Map function that sends the identity matrix to 1.

Formal Definition

1. Consider $M_{n\times n}$ as $({\mathbb{R}}^n{)}^m$ where the rows are thought as vectors in ${\mathbb{R}}^n$
2. If $f:M_{n\times n}(\mathbb{R})\to \mathbb{R}$ is
   1. Alternating
   2. Multilinear Map
   3. Satisfies $f(I)=1$ Then, $f=\det$

Properties

• $\det (I)=1$
• $\det (AB)=\det (A)\det (B)$
• $\det (A^k)=(\det (A){)}^k$
• If $A$ is $n\times n$ matrix, $\det (kA)=k^n\det (A)$
• $\det (A)=\det (A^T)$ where $A^T$ is the matrix transpose of $A$.
• $\det (A^{-1})=\frac{1}{\det (A)}$
• Interchanging two rows or columns multiplies the determinant by $(-1)$
• Multiplying a row by $k$ multiplies the determinant by $k$
• Adding a multiple of one row to another does not change the value of the determinant
• If two rows are identical than $\det (A)=0$
• $\det ([v_1,\dots ,v_n])=\text{ signed volume of parallelpiped by }\{v_1,\dots ,v_n\}$
• $\det (A)\ne 0⟺A$ Invertible

Theorems

• Determinants and Invertiblity Theorem
• Determinants and Row Operations
• Recursive Formula for Determinant
• Determinants and Eigenvalues
• Determinant from Permutations

Concepts

• Diagonal Matrices
• Determinant of 1x1 Matrix
• Determinant of 2x2 Matrix
• Determinant of Diagonal Matrix