Squeeze Theorem

Used primarily for evaluating limits in Trigonometric Functions, or any function that inherently has an upper & lower bound

Theorem

Let $L,c\in R$ and suppose there exists $d>0$ so that $f$, $g$ and $h$ are on a punctured interval at $c$. if:

1. $h(x)\le f(x)\le h(x)$
2. ${\lim }_{x\to c}g(x)={\lim }_{x\to c}h(x)=L$ Then ${\lim }_{x\to c}f(x)=L$ https://www.youtube.com/watch?v=2attRllfd-g

Proof

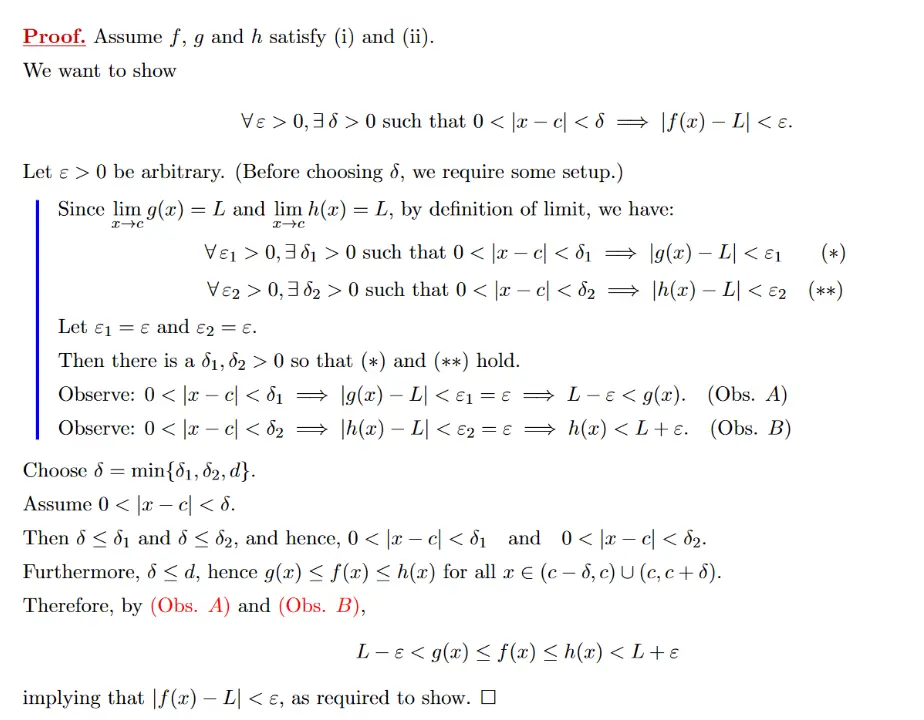
Tips

• If there is sine or cosine in the initial WTS, then you can use the innate range of them as boundings. For example, get $-1\le \cos x\le 1$ and then work from there to get real function you wanted to prove was less than $ϵ$

Examples

• Squeeze Theorem sinx over x
• Squeeze Theorem x squared times sin 1 over x