Differentiability

For a point to be differentiable and have a derivative, it must:

1. Be continuous at that point
2. Limit exists at $f^{\prime }(c)$. That is: $f^{\prime }(x^{-})=f^{\prime }(x)=f^{\prime }(x^{+})$

Formal Definition

$f$ is differentiable if at $a$, $f^{\prime }(x)$ exists. It is differentiable on an interval $I$ if it is:

• Differentiable at every point in the interior of $I$
• It is right differentiable on closed left endpoints
• It is left differentiable on closed right endpoints

Non Differentiable Cases

1. Cusp. Sharp change from left slope to right slope
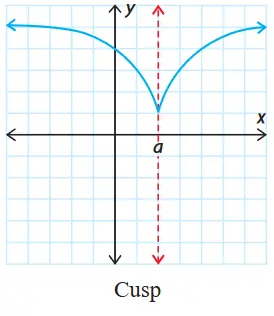
2. Vertical Tangent. Sharp change from left/right limits slope to actual slope(which is undefined)
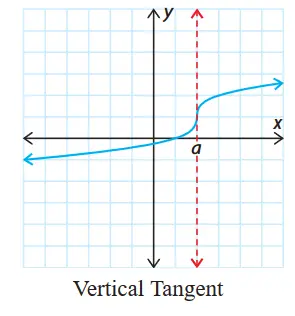
3. Discontinuity. Not continuous
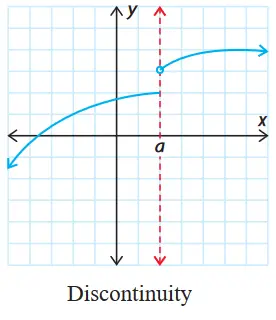
4. Absolute function point. Sharp change from left limit slope to right limit slope. Consult Absolute Function

Proving Non-Differentiable

Prove that the one-sided derivatives are different.

Differentiability $⟹$ Continuity

• Differentiable Implies Continuity Proof