Supremum

It is the least Upper Bound. Assumes the Completeness Axiom Most of the time it is the Max, but it can also exist if the maximum doesnt like cases $[0,5)$

Notation

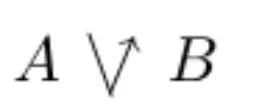Or $s=\sup (S)$

Definition

Let $S\subset R$ and $s\in R$, we say that $s$ is in the Supremum of $S$ if:

1. $s$ is an upper bound of $S$ ($\forall x\in S,x\le s$)
2. if $b$ is an upper bound of $S$, then $s\le b$

Alternate Definition (Approximation Theorem)

We can approximate $\sup (s)$ as close as we wish using elements of $S$. Given any tolerance $ϵ$, then the max - $ϵ$ is not an upper bound. Theorem: Assume $s$ is an upper bound of a non-empty set $S\subset R$, then $s=sup(S)⟺\forall ϵ>0,\exists x\in S$ s.t $s-ϵ<x$.

Proof:

Note $S\ne 0$ and is bounded above (since $s$ is an upper bound) so:

• $sup(S)$ exists by Least Upper Bound Property of Completeness Axiom ($⟹$) Assume $s=\sup (S)$ Let $ϵ>0$ be arbitrary. Let $b=s-ϵ$ We want to assume for contradiction that b is an upper bound. This means $\forall x\in S$, $s-ϵ\ge x$. $b<s$. This contradicts that $s$ is the least upper bound. Therefore $b$ is an upper bound is a contradiction. Thus $\forall x\in S,s-ϵ<x$ Thus $s=sup(S)⟹\forall ϵ>0,\exists x\in S,s-ϵ<b$ ($⟸$) Let $ϵ>0$ be arbitrary. Assume $\exists x\in S$ s.t $s-ϵ<x$ Assume for contradiction that $B$ is an upper bound and $B<s$ Then $B-B<s-B$ Then $0<s-B$ Choose $ϵ=s-B$ Then $s-(s-B)<x$ Then $=B<x$ This means that B is no longer a upper bound. This is a contradiction. So, our $B<s$ was a contradiction. Thus $B\ge s$ So $s\le B⟹s=sup(S)$

Concepts

• Least Upper Bound Property
• Proving Supremums