🍈 Zettelkasten

UIUCTF2024 Determined

5 min read

Challenge Resources

server.py:

from Crypto.Util.number import bytes_to_long, long_to_bytes
from itertools import permutations
from SECRET import FLAG, p, q, r
 
 
 
def inputs():
    print("[DET] First things first, gimme some numbers:")
    M = [
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
    ]
    try:
        M[0][0] = p
        M[0][2] = int(input("[DET] M[0][2] = "))
        M[0][4] = int(input("[DET] M[0][4] = "))
 
        M[1][1] = int(input("[DET] M[1][1] = "))
        M[1][3] = int(input("[DET] M[1][3] = "))
 
        M[2][0] = int(input("[DET] M[2][0] = "))
        M[2][2] = int(input("[DET] M[2][2] = "))
        M[2][4] = int(input("[DET] M[2][4] = "))
 
        M[3][1] = q
        M[3][3] = r
 
        M[4][0] = int(input("[DET] M[4][0] = "))
        M[4][2] = int(input("[DET] M[4][2] = "))
    except:
        return None
    return M
 
def handler(signum, frame):
    raise Exception("[DET] You're trying too hard, try something simpler")
 
def fun(M):
    def sign(sigma):
        l = 0
        for i in range(5):
            for j in range(i + 1, 5):
                if sigma[i] > sigma[j]:
                    l += 1
        return (-1)**l
 
    res = 0
    for sigma in permutations([0,1,2,3,4]):
        curr = 1
        for i in range(5):
            curr *= M[sigma[i]][i]
        res += sign(sigma) * curr
    return res
 
def main():
    print("[DET] Welcome")
    M = inputs()
    if M is None:
        print("[DET] You tried something weird...")
        return
 
    res = fun(M)
    print(f"[DET] Have fun: {res}")
 
if __name__ == "__main__":
    main()

gen.py:

from SECRET import FLAG, p, q, r
from Crypto.Util.number import bytes_to_long
n = p * q
e = 65535
m = bytes_to_long(FLAG)
c = pow(m, e, n)
# printed to gen.txt
print(f"{n = }")
print(f"{e = }")
print(f"{c = }")

gen.txt:

n = 158794636700752922781275926476194117856757725604680390949164778150869764326023702391967976086363365534718230514141547968577753309521188288428236024251993839560087229636799779157903650823700424848036276986652311165197569877428810358366358203174595667453056843209344115949077094799081260298678936223331932826351
e = 65535
c = 72186625991702159773441286864850566837138114624570350089877959520356759693054091827950124758916323653021925443200239303328819702117245200182521971965172749321771266746783797202515535351816124885833031875091162736190721470393029924557370228547165074694258453101355875242872797209141366404264775972151904835111

Solution

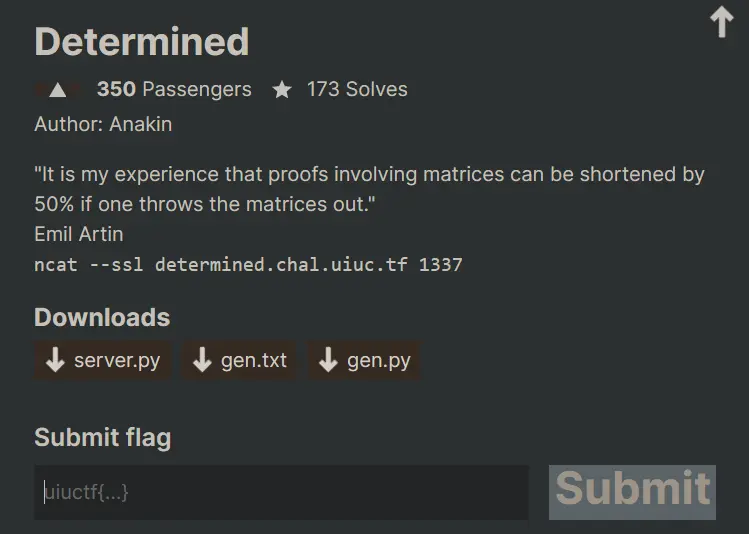
There are constants saved in a file n, p, r server.py takes in 9 inputs lets call them n1, n2, n3 … respectively and then arranges them in a matrix like fashion along with n, p, r 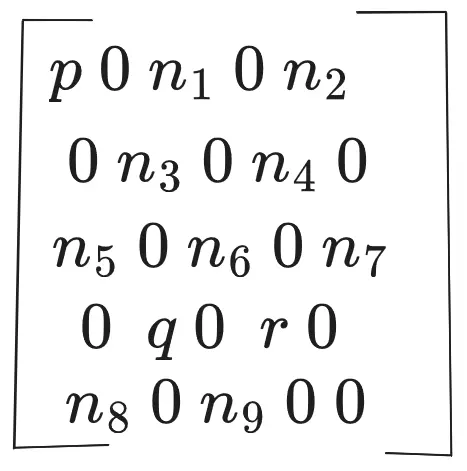Then, it runs this matrix through a fun() function which does some mathematical algorithm to return integer value result. When we run the netcat instance, we see this in practice here: 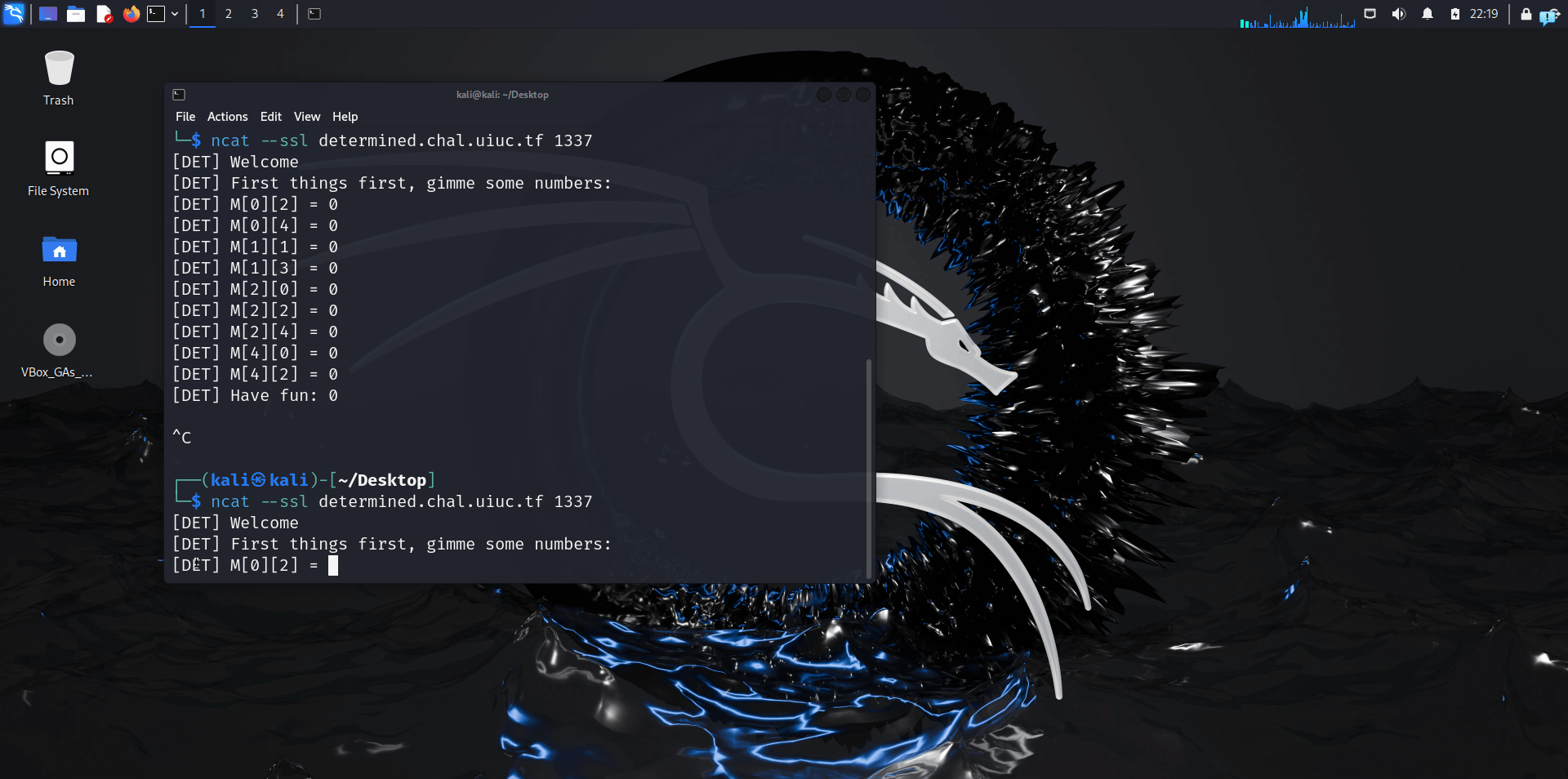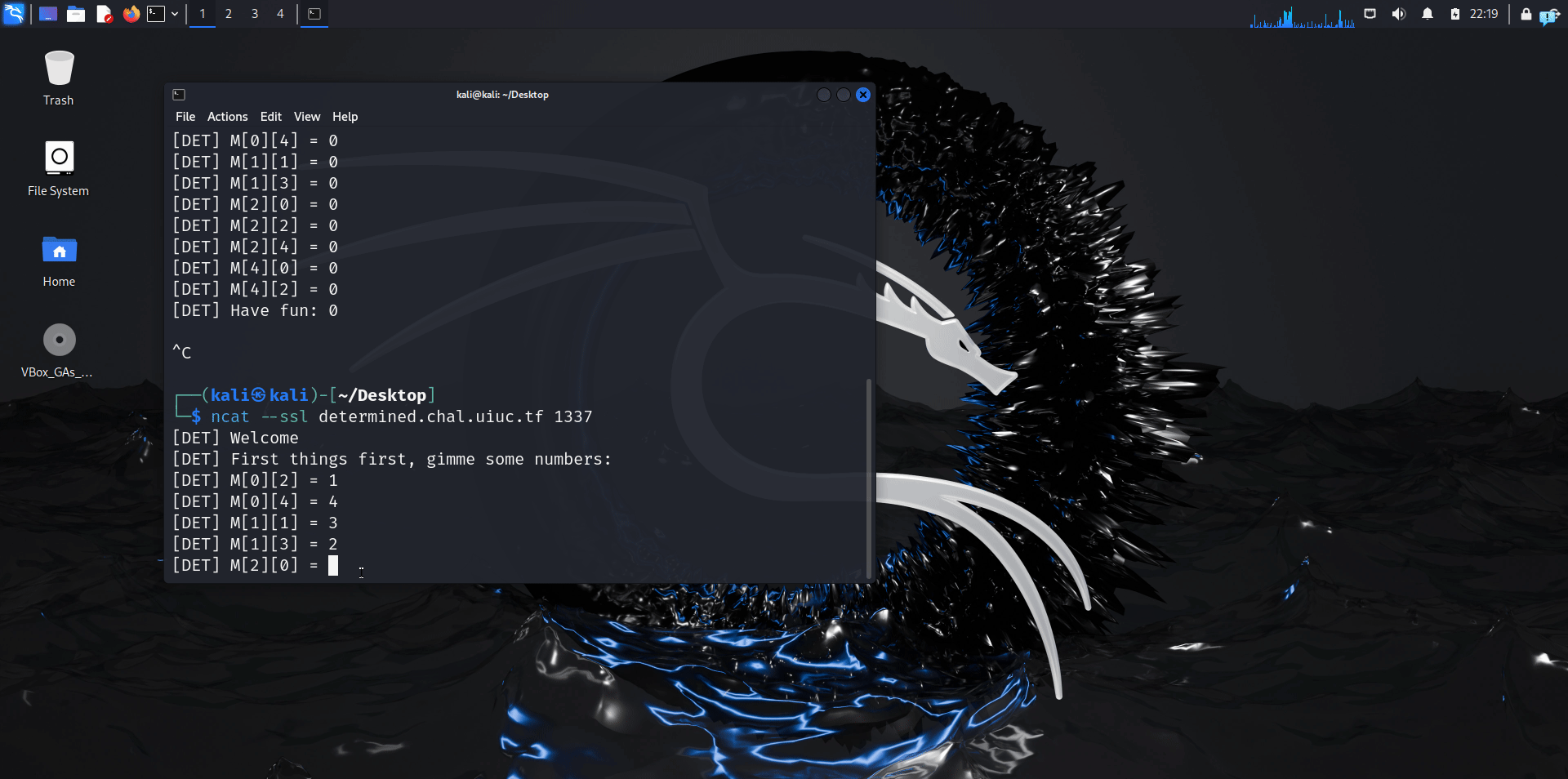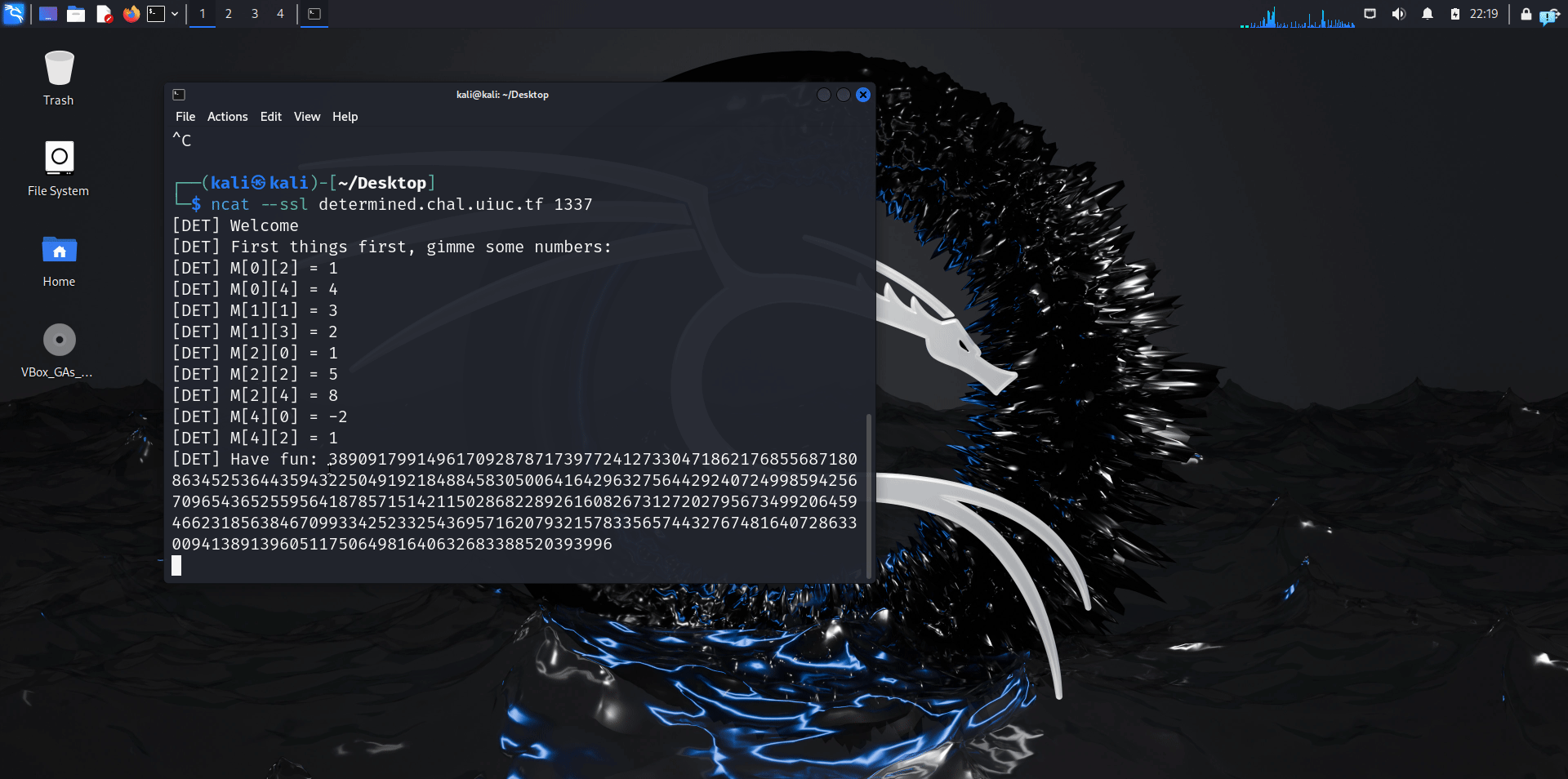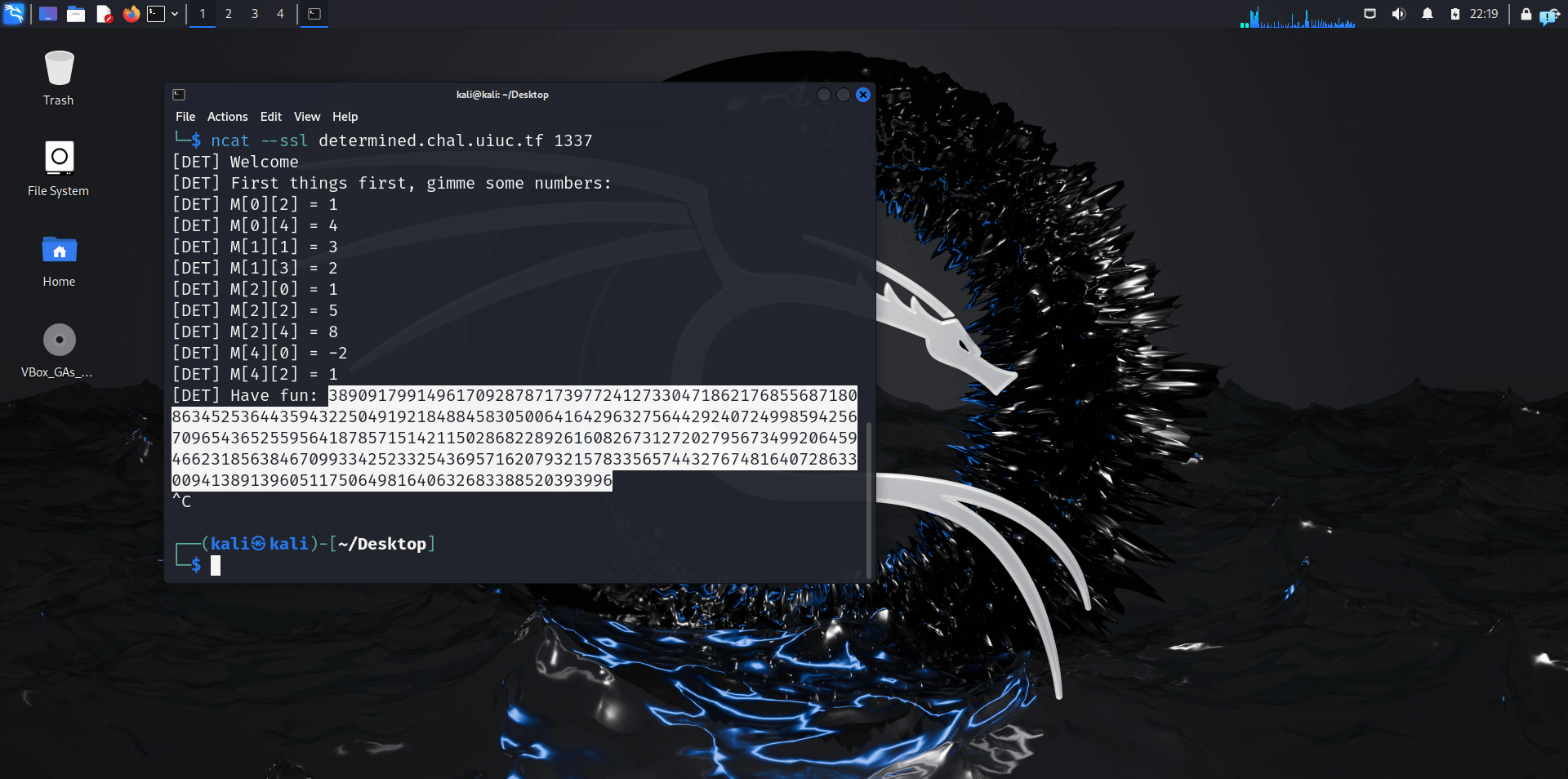When we simplify the fun() function, we see that result can be expressed as an equation:

result =
p * n3 * n9 * r * n7 * -1 +
p * q * n9 * n4 * n7 * 1 +
n5 * n3 * n9 * r * n2 * 1 +
n5 * q * n9 * n4 * n2 * -1 +
n8 * n3 * n1 * r * n7 * 1 +
n8 * n3 * n6 * r * n2 * -1 +
n8 * q * n1 * n4 * n7 * -1 +
n8 * q * n6 * n4 * n2 * 1

So far, we currently know:

  • the 9 n* and result are variables that we can determine the value of
  • the variables p, q and r are constant values we dont know

Lets, look at the gen.txt and gen.py files now. From those files, we are able to know:

m = bytes_to_long(FLAG)
 
n = p*q = 158794636700752922781275926476194117856757725604680390949164778150869764326023702391967976086363365534718230514141547968577753309521188288428236024251993839560087229636799779157903650823700424848036276986652311165197569877428810358366358203174595667453056843209344115949077094799081260298678936223331932826351
 
c = 72186625991702159773441286864850566837138114624570350089877959520356759693054091827950124758916323653021925443200239303328819702117245200182521971965172749321771266746783797202515535351816124885833031875091162736190721470393029924557370228547165074694258453101355875242872797209141366404264775972151904835111
 
c=m^65535 % p*q

Thus, we now know:

  • the 9 n*
  • the value of result
  • the value of p*q
  • the value of c we don’t know:
  • r
  • individual values of p and q
  • most importantly, the value of m

Understanding the ‘c’ equation

c=m^65535 % p*q how can we reverse this? This is actually the RSA Problem. We just need the values of p and q I tried Chinese Remainder Theorem, and it didn’t work. There is another method, we can use though.# If we can obtain the r, value and use the concrete value instead of r’s symbolic value, then the result equation will be in terms p and q. Then, we can compare n and result to obtain the values of p and q

Obtaining ‘r’ value

Remember that If we can find the correct n* values that cancel out p and q terms, we can make result equal to terms of r, then we can find r. A possible pair for this is: n2=0,n4=0,n9=0 and all other n*=1 where result=r another possible pair for this is: n4=0,n6=-1,n7=0 and all other n*=1 where result=2r So, we find that the value of r when we do this on the server is:

r = 7079077828991557904453386075761691430024858841559152638771101891403817504002722603786046116429444882212741713778792076162641378721868400698674834419068143

Obtaining ‘q’

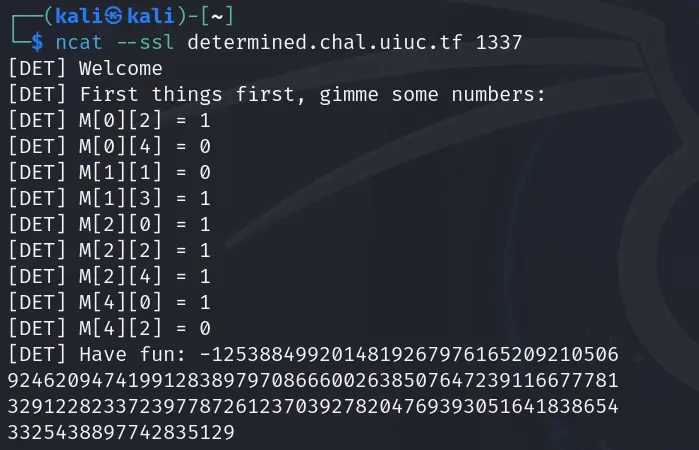
If we make n2,n3,n9 = 0 then, result = -q. So, we do that and get q = 12538849920148192679761652092105069246209474199128389797086660026385076472391166777813291228233723977872612370392782047693930516418386543325438897742835129

Obtaining ‘p’

Now, that we have q, we can solve for p, as n=pq use this https://www.mathsisfun.com/calculator-precision.html When we do p = n/q, we find: p=12664210650260034332394963174199526364356188908394557935639380180146845030597260557316300143360207302285226422265688727606524707066404145712652679087174119

Using RSA Solver

This is the RSA solver I used for finding totient, generated with Phind.

from sympy import mod_inverse
# Given values
n = 158794636700752922781275926476194117856757725604680390949164778150869764326023702391967976086363365534718230514141547968577753309521188288428236024251993839560087229636799779157903650823700424848036276986652311165197569877428810358366358203174595667453056843209344115949077094799081260298678936223331932826351
e = 65535
c = 72186625991702159773441286864850566837138114624570350089877959520356759693054091827950124758916323653021925443200239303328819702117245200182521971965172749321771266746783797202515535351816124885833031875091162736190721470393029924557370228547165074694258453101355875242872797209141366404264775972151904835111
q = 12538849920148192679761652092105069246209474199128389797086660026385076472391166777813291228233723977872612370392782047693930516418386543325438897742835129
p = 12664210650260034332394963174199526364356188908394557935639380180146845030597260557316300143360207302285226422265688727606524707066404145712652679087174119
 
# Calculate phi(n)
phi_n = (p - 1) * (q - 1)
# Find d, the modular multiplicative inverse of e modulo phi(n)
d = mod_inverse(e, phi_n)
# Decrypt c to get m
m = pow(c, d, n)
 
print(f"The original message is: {m}")

And we find that m = 3480415922530522028140788720602089153725974401135124317590588599653485642863636093

Converting Long to String

I used this longtostring python script:

from Crypto.Util.number import long_to_bytes
 
val = 3480415922530522028140788720602089153725974401135124317590588599653485642863636093
original_bytes = long_to_bytes(val)
print(original_bytes)
original_string = original_bytes.decode('utf-8')
print(original_string,end="")

And we find the final flag is: uiuctf{h4rd_w0rk_&&_d3t3rm1n4t10n}

Graph View