Trig Identities

Table of Contents

Identity

An identity is something valid for ALL values of x. They can ALL be proved.

If they cannot be proved, show a counter example by subbing in a value for x

List of Identities (*) are important ones

• Transformation Identities
• Even and Odd Identities *
• Supplementary Function Identities *
• Co-Function Identities *
• Compound Angle Identity *
• Double Angle Identity *
• Reduction Identity
• Half Angle Identity *
• Sum to Product
• Product to Sum

Practical Identity Use

• Random Angle to Co-Function or Supp-Function Identity
• Equivalent Ratio Problem Solving Procedure ⇐ Good for understanding Co-Function

Proving Identities Techniques

General

• Separate LS and RS. You cannot cross terms between sides
• Try to change everything into terms of sin and cos
• Find common denominators
• Use Difference of Squares.
• Use power rule.
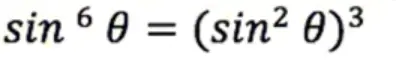
• Use more Transformation Identities during simplification
• Multiply by 1 if required

Specific

• If you see (1-cos),(1+cos),(1-sin),(1+sin) in the denominator, try multiplying the numerator and denominator by the conjugate. eg, conjugate of (1-cos) = (1+cos).
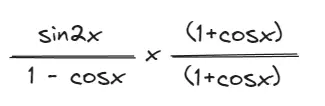
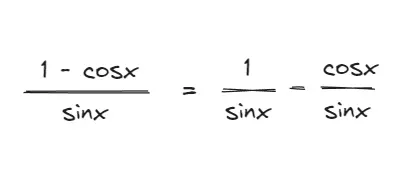
  • If you see a fraction with 2 terms in numerator and 1 term in denominator, split that fraction in 2. parts