Normal Distribution Test Review

Question 1

On a cherry farm, 5% of cherries are more than 8.5g. 7% of cherries are less than 5.1g. If the masses of cherries can be normally distributed, determine probability of cherries that are over 7.0g

Solution

P(x>8.5) = 0.05 P(x<5.1) = 0.07 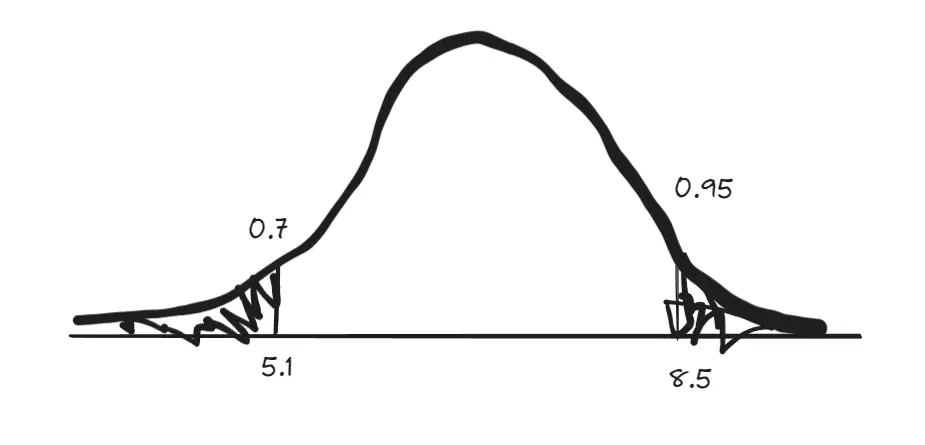z score of 0.07 = -1.475 -1.475 = $\frac{x-\mu }{\sigma }$ -1.475 = $\frac{5.1-\mu }{\sigma }$ $-1.475\sigma =5.1-\mu$ $\mu =1.475\sigma +5.1$ z score of 0.95 = 1.645 1.645 = $\frac{8.5-\mu }{\sigma }$ $1.645\sigma =8.5-\mu$ $\mu =-1.645\sigma +8.5$

$(1.475\sigma +5.1)-(-1.645\sigma +8.5)$ $0=3.12\sigma -3.4$ $\sigma =1.08974$ $\mu =1.475(1.08974)+5.1=6.7073$ $\mu =6.7073$

find probability from z-score of 7.0 $z=\frac{7-6.7073}{1.08974}=0.2685$ z-score to probability 0.605. 1 = 0.605 = 0.395 0.395% of cherries are over 7.0g

Question 2

A machine produces articles. average of 2% of articles are defective. in a batch of 400 articles, what is the probability that there are fewer than 5 that are defective?

Solution

You can use binomial if you want. $\mu =0.02(400)=8>5$ first case fuffiled $nq=392$ > 5. second case fufilled we can use continuous! $\sigma =\sqrt{400\ast 0.02\ast 0.98}=2.8$ P(x<5) = P(x<4.5) P(z<$\frac{4.5-8}{2.8}$) P(z<$-1.25$) = $0.10565$ 10.565 articles will be wasted