Critical Points

Table of Contents

Critical Points

1. $c$ is in the domain of $f(x)$
2. either $f^{\prime }(x)=0$ or $f^{\prime }(x)$ is undefined. Then $(c,f(c))$ is a critical point. From these, you can get global maximas/minimas

Maxima/Minima

Maximas and minimas exist within a range, where there are limits for all defined values inside the range.

Maxima

c is the maxima if $f(x)\le f(c)$ for all $x$ in the domain of $f(x)$

Minima

c is the minima if $f(x)\ge f(c)$ for all $x$ in the domain of $f(x)$

Global Maxima/Minima

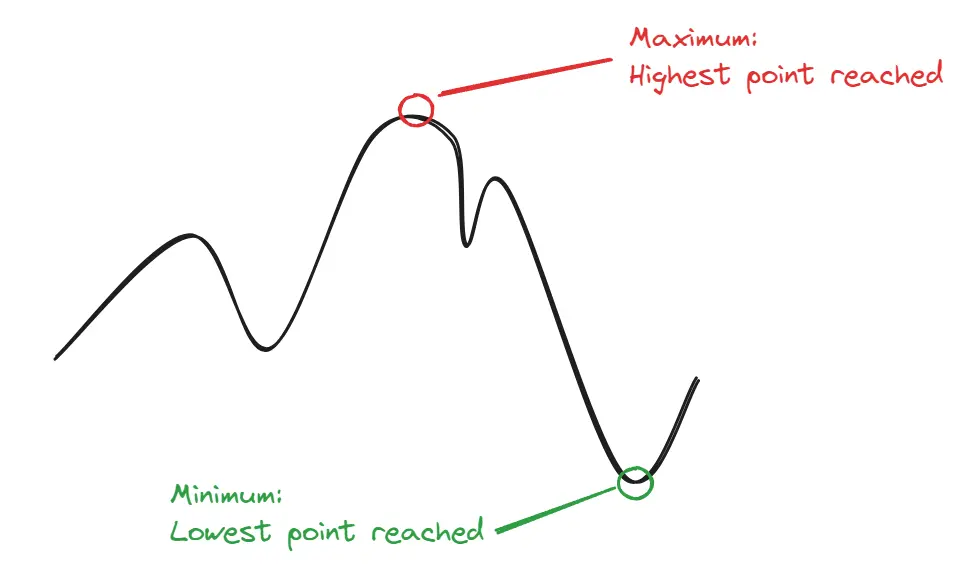
• Must be restricted on an interval
• $0\le globalmin/max\le \infty$. You can have infinite global mins/max
• Can be called local & global max

Local Maxima/Minima

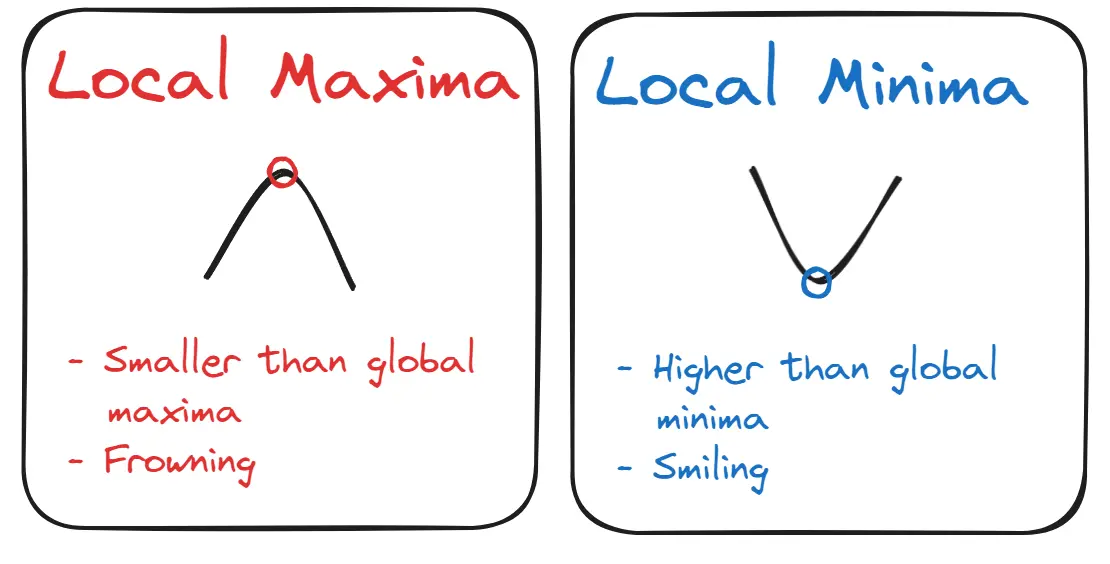A turning point that is NOT the global maxima/minima

Concepts

• Fermat’s Theorem Stationary Points

2nd Derivative Test

For a critical point,

• if $f^{\prime \prime }(x)<0$, the point is a local maximum
• if $f^{\prime \prime }(x)>0$, the point is a local minimum
• if $f^{\prime \prime }(x)=0$, a local maxima/minima does not exist

Procedure for finding maxima/minima

1. Find the possible points. These are:
   • Critical Points within the interval
   • Endpoint values. (The points at the boundaries of the interval)
2. 2nd Derivative test for each found point
3. Largest point is maxima. Smallest is minima