Of a factored form polynomial, it is built in the form: a(x-d)(x-e)… with a being the vertical stretch. So far, we know how to get the factors using Orders in tandem with Bounce and Cross, but we have yet to figure out the vertical stretch of the function.
The method
So say you have this graph.
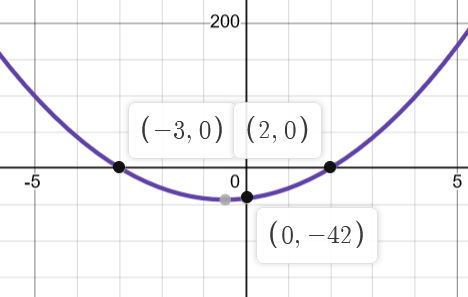So far, you know the equation is: f(x) = a(x-2)(x+3) just from the X Intercepts
The question is, what is a?
The one point that we know for sure other than the X Intercepts is the Y Intercept
Thus we can use that in our formula.
-42 = a(0-2)(0+3)
-42 = a(-2)(3)
-42 = a(-6)
a = 7
Approximation
Certain times you may not be able to precisely see the Y intercept value.
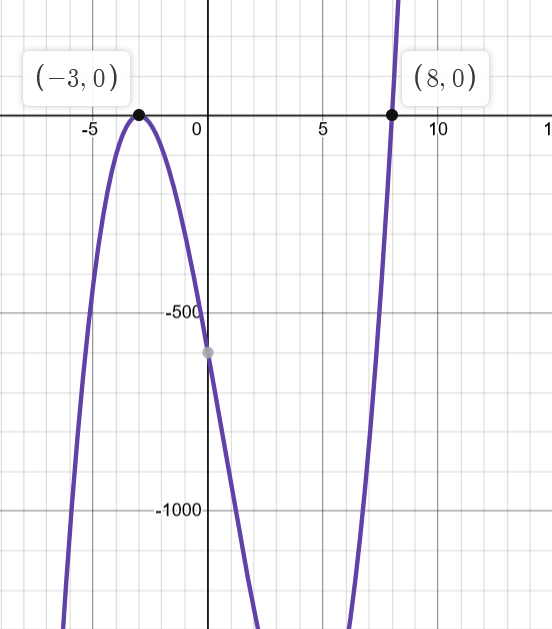In these rare cases, it would be wise to approximate the Y intercept rather than find it.
y ~ -600
-600 ~ a(x+3)^2(x-8)
-600 ~ a(9)(-8)
-600 ~ a(-72)
a ~ 8.333333333333