Magic Square

A 2x2 matrix in which the sum of all columns, rows and diagonals equals to the same number.

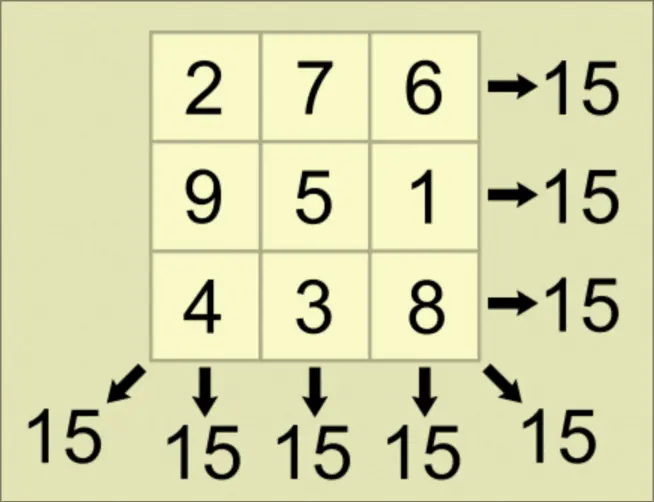
• Each entry is a distinct item in $\{1,2,\dots ,n^2\}$
• Where the magic constant that all rows and columns sum to is equal to $M=\frac{n(n^2+1)}{2}$

Solving Magic Square with C Program

////////////////////////////////////////////////
// CSC A48 - Exercise 5 - Solving Magic Squares
//
// (c) F. Estrada
////////////////////////////////////////////////
#include<stdio.h>
#include<stdlib.h>
 
 
void solveMagicSquare(int square[6][6])
{
  // we assume that atleast one row/column has the magic constant as the sum. if not, then this matrix is unsolvable
  int constants[12];
  int constants_counter = 0;
  int unknowns_to_solve = 0;
  // rows
  for (int row = 0; row < 6; row++){
    int tempsum = 0;
    for (int col = 0; col < 6; col++){
      tempsum += square[row][col];
      // adding unknowns number
      if (square[row][col] == -1){
        unknowns_to_solve++;
      }
    }
    constants[constants_counter] = tempsum;
    constants_counter++;
  }
  // columns
  for (int col = 0; col < 6; col++){
    int tempsum = 0;
    for (int row = 0; row < 6; row++){
      tempsum += square[row][col];
    }
    constants[constants_counter] = tempsum;
    constants_counter++;
  }
  // diagonals
  int tempsum = 0;
  for (int i = 0; i < 6; i++){
    tempsum += square[i][i];
  }
  constants[constants_counter] = tempsum;
  constants_counter++;
  tempsum = 0;
  for (int i = 5; i >= 0; i--){
    tempsum += square[5-i][i];
  }
  constants[constants_counter] = tempsum;
  constants_counter++;
 
  // find the maximum magic constant
  int magic_const = 0;
  for (int i = 0; i < constants_counter; i++){
    if (constants[i] > magic_const){
      magic_const = constants[i];
    }
  }
  //printf("magic const is: %d\n", magic_const);
  //printf("number of unknowns: %d\n", unknowns_to_solve);
  // try to solve for the rows/columns/diagonals with only one -01 first
  int num_is = 0;
  int i_index = 0;
  int row_sum = 0;
  while (unknowns_to_solve > 0){
    // check each row for single -1
    //printf("checking rows, unknowns_to_solve is: %d\n", unknowns_to_solve);
    for (int row = 0; row < 6; row++){
      num_is = 0;
      i_index = 0;
      row_sum = 0;
      for (int col = 0; col < 6; col++){
        //getting number of 1s
        if (square[row][col] == -1){
          num_is++;
          i_index = col;
        }
        else {
          row_sum += square[row][col];
        }
      }
      // 1. check if only one -1
      if (num_is == 1){
        square[row][i_index] = magic_const - row_sum;
        unknowns_to_solve--;
      }
    }
    // check each column for single -1
    //printf("checking columns, unknowns_to_solve is: %d\n", unknowns_to_solve);
    for (int col = 0; col < 6; col++){
      num_is = 0;
      i_index = 0;
      row_sum = 0;
      for (int row = 0; row < 6; row++){
        //getting number of 1s
        if (square[row][col] == -1){
          num_is++;
          i_index = row;
        }
        else {
          row_sum += square[row][col];
        }
      }
      // 1. check if only one -1
      if (num_is == 1){
        square[i_index][col] = magic_const - row_sum;
        unknowns_to_solve--;
      }
    }
    // check each diagonal for single -1
    //printf("checking diagonals, unknowns_to_solve is: %d\n", unknowns_to_solve);
    row_sum = 0;
    num_is = 0;
    i_index = 0;
    for (int i = 5; i >= 0; i--){
      if (square[5-i][i] == -1){
        num_is++;
        i_index = i;
      }
      else{
        row_sum += square[5-i][i];
      }
    }
    if (num_is == 1){
        square[5-i_index][i_index] = magic_const - row_sum;
    }
    // other diagonal
    //printf("checking diagonals, unknowns_to_solve is: %d\n", unknowns_to_solve);
    row_sum = 0;
    num_is = 0;
    i_index = 0;
    for (int i = 0; i < 6; i++){
      if (square[i][i] == -1){
        num_is++;
        i_index = i;
      }
      else{
        row_sum += square[i][i];
      }
    }
    if (num_is == 1){
        square[i_index][i_index] = magic_const - row_sum;
    }
 
    //printf("current iteration done with unknowns_to_solve: %d\n", unknowns_to_solve);
  }
 
}
 
  
 
 
 
 
// DO NOT MODIFY ANYTHING BELOW THIS LINE!
// (we mean it! the auto-checker won't be happy)
void printMagicSquare(int square[6][6])
{
   // Prints out the contents of a magic square 6x6
 
   int i,j,sum;
 
   for (i=0; i<6; i++)
   {
       sum=0;
       for (j=0; j<6; j++)
       {
           printf("%03d, ",square[i][j]);
           sum=sum+square[i][j];
       }
       printf(" : %03d\n",sum);
   }
 
   printf("---------------------------\n");
 
   for (j=0; j<6; j++)
   {
       sum=0;
       for (i=0; i<6; i++)
       {
	   sum=sum+square[i][j];
       }
       printf("%03d, ",sum);
   }
   printf("\n");
}
 
#ifndef __testing   // This is a compiler directive - used by the auto-checker to enable/disable this part of the code
int main()
{
    int magic[6][6]={{32,29,4,1,24,21},{30,-1,2,3,-1,23},{12,9,17,20,28,25},{10,11,18,-1,26,27},{13,-1,36,33,5,8},{14,15,34,35,6,-1}};
 
    printMagicSquare(magic);
    printf("Solving Magic Square!\n");
    solveMagicSquare(magic);
    printMagicSquare(magic);
 
    return 0;
}
#endif