A ECC that is able to detect 2-bit errors and fix 1-bit errors. Uses parity bits and parity circles to determine where errors occur.
Notation
- Encodes -input bits into -output bits
- Adds extra parity parity bits Theoretically, for parity bits, you can have data bits
Process (Hamming (7,4))
Sending Process
- Create your 4-bit message, then encode with a hamming encoding algorithm (Maybe Hamming (7,4))
- For Hamming (7,4), we have the encoding matrix:
1 & 0 & 0 & 0\ 0 & 1 & 0 & 0\ 0 & 0 & 1 & 0\ 0 & 0 & 0 & 1\ 0 & 1 & 1 & 1\ 1 & 0 & 1 & 1\ 1 & 1 & 0 & 1\ \end{array}\right]$$ 3. Then, with our message, lets say , encoded is 4. In our case,
Recieving Process
- Given the message, calculate the sum of each circle for the recieved message by left multiplying vector
- where:
- is the parity of each circle
- is the location of each bit in the circles
- Bob calculates to get
- If contains non-zero entries, then there is an error
- If one error occured, then the error is precisely at location
- If (one of the message bits was ruined) then would be the corrected message
- If (one of the parity bits was ruined), then we can just ignore it
- Alternatively, finding through the diagram, the wrong bit, first find the two circles that are invalid, then the wrong bit is at the intersection between the two circles
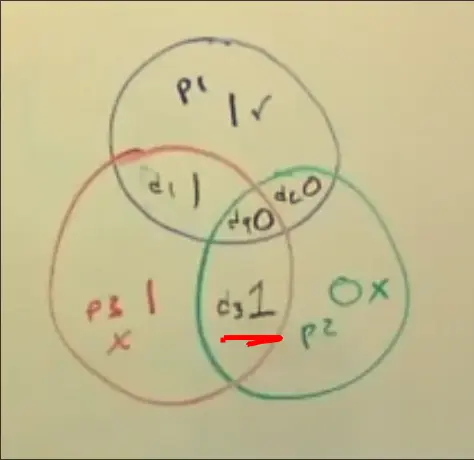
- If one error occured, then the error is precisely at location