Riemann Sums

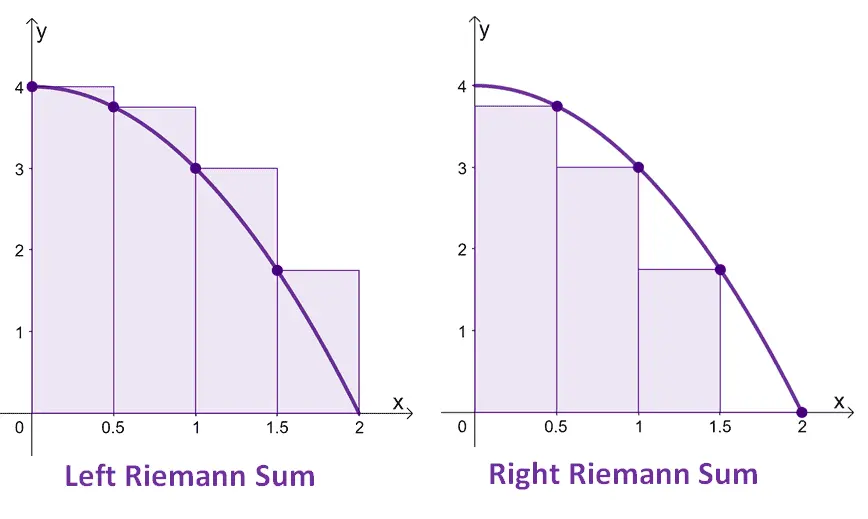
Used for adding up the areas of the rectangles Signed Area of a function from below between two points $[a,b]$. Riemann Partitions break the function bodies into several rectangles whose areas are added

Continuity ‘Requirement’

Riemann sums can be applied without any setup however, it should be noted that:

• A converging Riemann sum requires $f(x)$ to be Continuous
• if $f(x)$ is Discontinuous, then a accurate riemann sum is not guaranteed

Notation

${\sum }_{i=1}^{n}f(x_i^{\ast })△x$

• n signifies the number of partitions
  • Conjecture: The larger the $n$ value, the more accurate the Riemann sum estimation
• Conjecture: if $f(x)$ is increasing on $[a,b]$, $L_n\le A\le R_n$
• Conjecture: if $f(x)$ is decreasing on $[a,b]$, $R_n\le A\le L_n$
• $△x=\frac{b-a}{n}$
• $x_i^{\ast }$ is the Riemann Partition for $x_i=a+i△x$
  • $x_i^{\ast }=x_{i-1}$ for Left Riemann Sum
  • $x_i^{\ast }=x_i$ for Right Riemann Sum
  • $x_i^{\ast }=\frac{x_{i-1}-x_i}{2}$ for Midpoint Riemann Sum

Riemann Sum Types

• Left Riemann Sum
• Right Riemann Sum
• Midpoint Riemann Sum

Classifications

• Upper Riemann Sum
• Lower Riemann Sum
• Trapezoid Riemann Sum

Concepts

• Reverse Engineering Riemann Sums