Linear Transformation Rotation

Given a linear map $R_e:{\mathbb{R}}^2\to {\mathbb{R}}^2$ We can express $R_e(x,y)$ for a given $(x,y)$ vector as: $R_e(x,y)=(x\cos (\theta )-y\sin (\theta ),y\cos (\theta )+x\sin (\theta ))$

Intuition

Drawing 2025-02-07 11.26.28.excalidraw

⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠

Text Elements

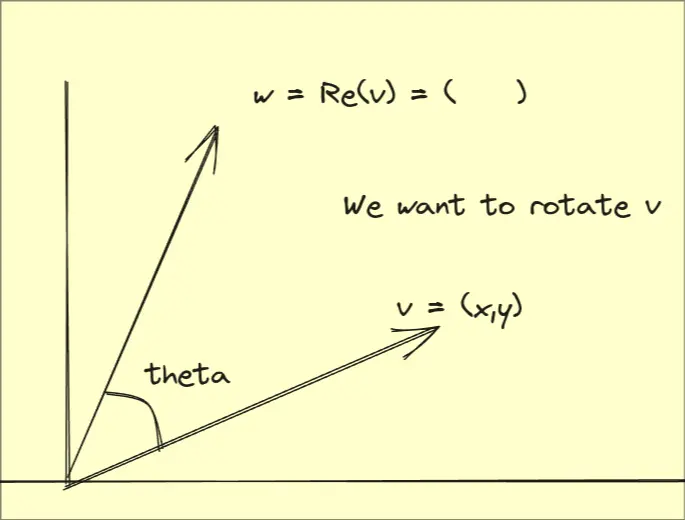
v = (x,y)

theta

w = Re(v) = ( )

y = || v || sin(d)

d

y = || v || cos(d)

Supposing v = (x,y) = (||v|| cos(x), ||v|| sin(x)

Then, we have Re(v) = (||v|| cos(d+theta), ||v|| sin(d + theta))

= (||v|| ( cos(d)cos(theta) - sin(d)sin(theta) ), ||v|| (sin(d)cos(theta) + sin(theta)cos(d)) )

by compound angle identity

= ( (||v||cos(d))cos(theta) - (||v||sin(d))sin(theta) , (||v||sin(d))cos(theta) + sin(theta)(||v||cos(d))

= (xcos(theta) - ysin(theta) , ycos(theta) + xsin(theta))

Link to original

Thus, our final formula is: $(x\cos (\theta )-y\sin (\theta ),y\cos (\theta )+x\sin (\theta ))$

Useful Rotations

${\mathbb{R}}^2$ y-axis reflection

$$\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$$

${\mathbb{R}}^2$ x-axis reflection

$$\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$$

${\mathbb{R}}^2$ Counter-Clockwise Rotation from Origin

$$\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

${\mathbb{R}}^2$ Reflection about $y=mx$

$$\frac{1}{1+m^2}\left[\begin{array}{cc}1-m^2& 2m\\ 2m& m^2-1\end{array}\right]$$

Reflection of $y=x$

$$\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$$

Reflection of $y=-x$

$$\left[\begin{array}{cc}0& -1\\ -1& 0\end{array}\right]$$