Determined only with Standard Form A function can have very consistent characteristics if it is even or odd. Not to be confused with even/odd Degree. An Even or Odd function is a function where every exponent satisfies a rule
Even Functions
A function is even when: f(x) = f(−x) for all x values
A function of which all exponents are even can look as such:
f(x) = x^4 = 2x^2 + 86 is an even function
This is because the exponents are: 0, 2 and 4.
And all of those are even.
of this function can be anything
Characteristics
An Even function will always look like a quadratic function with end behaviors like
Q2→Q1 or Q3→Q4.
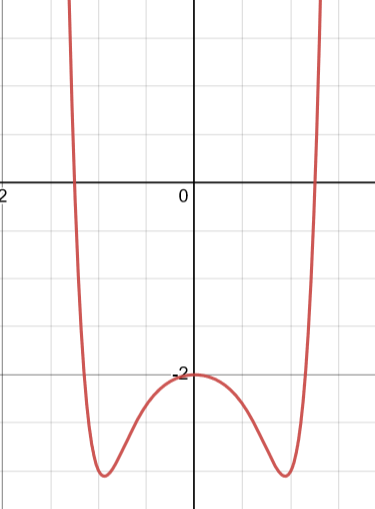
Equation above is: y=x^{8}-x^{4}-x^{2}-2
There is symmetry. Symmetry is about the Y axis ALWAYS. X=0 ALWAYS.
This means that when the X’s are be negative WILL result in the same Y values as the positive X
Odd Functions
A function is odd when: -f(x) = f(−x) for all x values
This only happens if each exponent in the polynomial Standard Form is of odd exponent.
f(x) = 3x^3 + x is an odd function because the only exponents are: 3,1. all of which are odd.
always.
Characteristics
End behaviors are similar to y=x linear functions.
from Q3→Q1 or Q2→Q4.
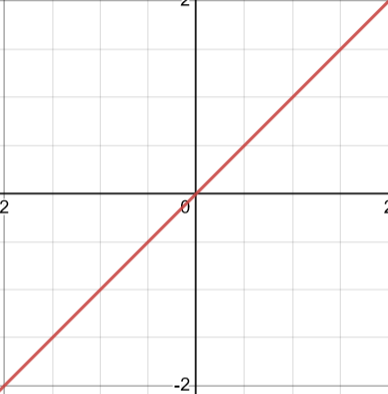The symmetry is about the origin
There is no symmetry. Functions when the X’s are negative WILL NOT result in same Y values as the positive X