Not all graphs have symmetry, but for those that do, they are either on a line or a point, or in 3d, a plane.
Look at these graphs:
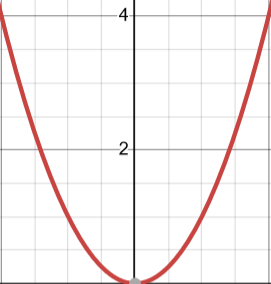
One is y=x^2 other is y=x^3
so, its apparent that the symmetry for y=x^2 is x=0.
the symmetry for y=x^3 is at origin. At origin because no matter what line you slice it from that includes origin, it will be symmetrical.
Symmetry After Transformation
y = a[k(x-d)^n]+c
Even functions
Vertex: (d,c) Axis of symmetry: x=d
for a > 0, graph opens up. the min is c and range is y >= c for a < 0, graph opens down and max is c and range is y ⇐ c
Odd functions
There are no vertex in odd functions There is only point symmetry in odd functions