Bounce and Cross

Order 2,4,6… even order factors have bounces on the graph. Order 1.3.5… odd order factors will cross on the graph Order 0 we don’t care about because it is impossible to have order 0 in a factored form polynomial.

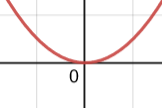
For Turning Points, to determine how the line will cross the x Intercept, Even orders will Bounce at the x-axis 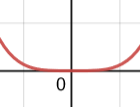Odd orders will Cross at the x-axis

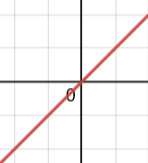
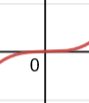
Example

So, say I have a factored polynomial like such: f(x) = (x-1)(x+7)^2(x-2) The factors are:

• (x-1) : Order 1
• (x+7)^2 : Order 2
• (x-2) : Order 1 Every Odd order x intercept will cross it. The sign changes Every Even order x intercept will bounce on it. The sign does not change Thus:
• (x-1) : Cross
• (x+7)^2 : Bounce
• (x-2) : Cross