**# Table of Contents

Rational Functions

A function in the form of f(x) = P(x)/Q(x).

Denominator stipulations

• Q(x) $\ne 0$
• Q(x) $\ne$ constant. Because dividing P(x) by a constant results in a single polynomial. eg. $\frac{2x^2+4x-8}{2}$ = $x^2+2x-4$

Asymptote

Values of x or y which the INFINITIES of the graph will never approach. INFINITIES because, Cross Over Points exist

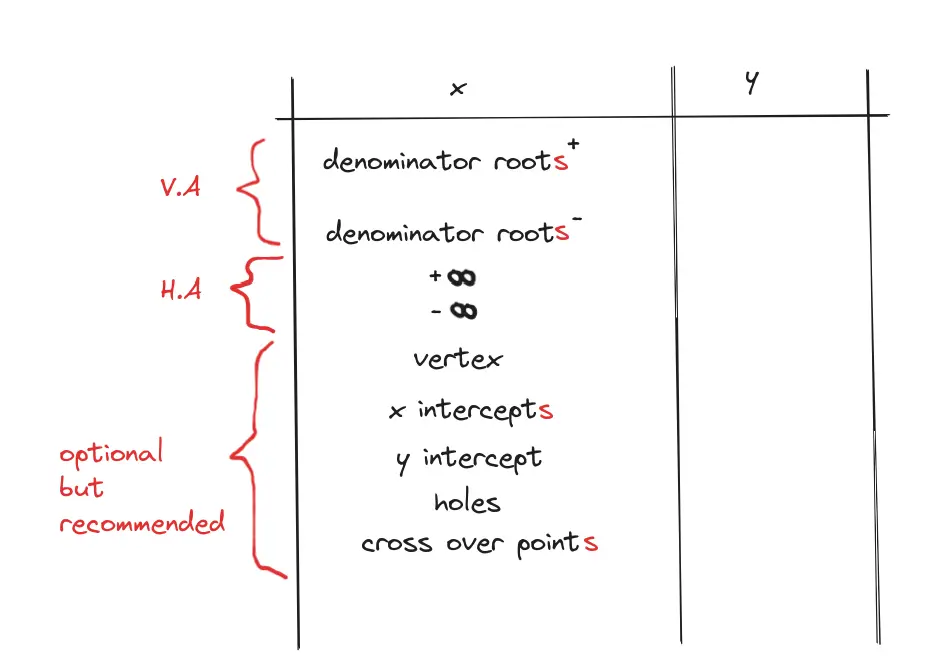
Vertical Asymptote (x=?)

When denominator equals 0.

Horizontal Asymptote (y=?)

with a rational function in standard form: $\frac{a{x}^m+\dots }{b{x}^n+\dots }$ if m < n, y = 0 if m > n, NO HA. You have a oblique or parabolic depending on the difference in degree if m = n, y = a/b

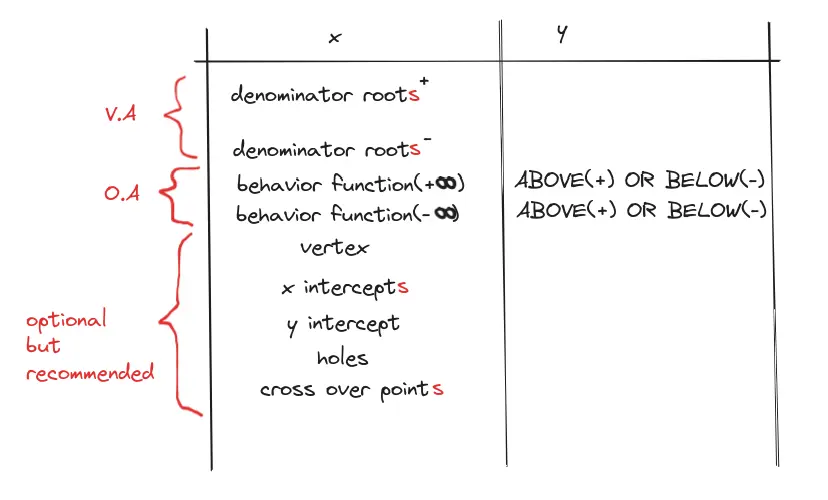
Oblique Asymptotes (y=ax^?+bx^?+cx^?…)

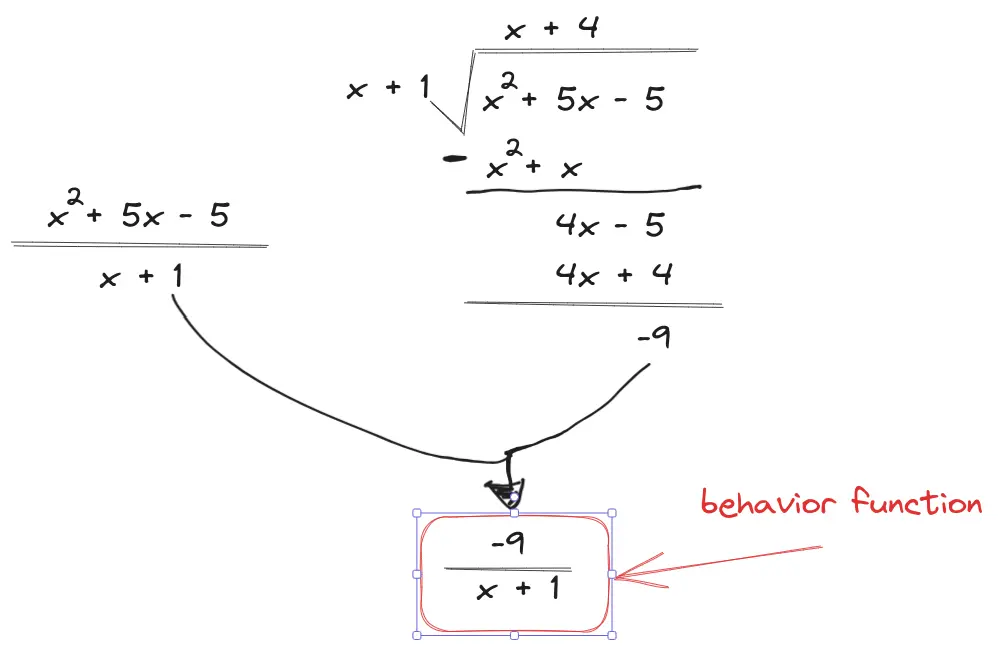
Occurs when the numerator has a higher degree than the denominator. It is the quotient of numerator/denominator. Find it through Long division You can use Test Points to determine how to graph an oblique asymptote

Hole

A special Asymptote of a coordinate that the graph will never reach. Occurs when you have a rational function where the numerator and denominator cancel out.

Cross Over Points

Points which cross the H.A or O.A To get this, simply make an equation setting the function equal to the H.A/O.A, then solve.

Behaviors

You have two

Behavior Table Method

Modified Behavior Table Method

Behavior Function

Rational Inequalities

Nothing much to say here. Solving Rational Inequalities